中学数学の因数分解の解き方｜やり方の流れとテクニックを解説

中学3年生の「数学」の授業で習う、中学数学の中で最も重要な公式・考え方の1つである「因数分解」。公式の種類も多く、複雑な計算が求められることも多いため、苦手意識を持っている人も多いでしょう。

因数分解（いんすうぶんかい）とは、式を足し算や引き算の形から、かけ算（積）の形に変形することをいいます。

この「因数分解」はこれからいろいろな数学の問題を解いていく上で非常に重要な公式となります。因数分解ができなければ、高校数学やその先の数学を戦うことはできないのです。

そのために今回は、因数分解とはいったいどのようなものなのかについて、そして因数分解が何に活かされるのかについて、実際の問題も入れながら解説していきます。因数分解に少しでも苦手意識がある人はぜひお読みください！

因数分解とは

因数分解（いんすうぶんかい）とは、式を足し算や引き算の形から、かけ算（積）の形に変形することです。例えば「2x+6」という式は、共通の因数である「2」でくくることで「2(x+3)」と表現できます。

このように一つの式を積の形にまとめ直す操作が「因数分解」です。

といっても、あまりピンとこない人も多いでしょう。「因数分解」について深く理解するために、まずは「因数」とは何なのかについて説明します。

因数とは

因数（いんすう）とは、「式を作るもと」となる数や文字式のことです。簡単な例として、まずは「整数」の因数を考えてみましょう。

たとえば「30」という数は、かけ算の形で表すと次のように分解できます。

30 = 2×3×5

この場合、かけ算の一つひとつの要素である 2、3、5 を「30の因数」と呼びます。つまり、因数とはかけ合わせて元の数や式になる要素のことです。

この法則は、文字を含む式でも同様です。例えば 「6x」 という式（これを単項式と呼びます）は次のように分解できます。

6x = 2×3×x

この場合、2、3、そしてxが「6x」の因数になります。

整数でも文字式でも、元の式を構成しているパーツ（数字や文字）が「因数」です。

なぜ因数分解するのか

「どうして因数分解を習う必要があるのか」と疑問に思う人も少なくないでしょう。因数分解を学習する大きな理由の一つは、「方程式を解きやすくするため」です。

中学3年生になると、x2の項が出てくる2次方程式（二乗を含む方程式）が登場します。例えば、

x2+5x+6=0

というような2次方程式は、そのまま解くことは非常に困難ですが、因数分解を使うと簡単に解くことができます。この式の左辺を因数分解して (x+2)(x+3)=0の形にできれば、それぞれの因数が0となる条件から解は

x = -2, -3

とすぐに求めることができます。このように、式をかけ算の形にしておくと、値を求めたり計算を簡単にしたりできるのです。

ちなみに、二次方程式を解く方法は基本的に、

• 平方根で考える
• 解の公式で考える
• 因数分解で考える

という3通りがあります。

この問題は「解の公式」を使ったり、平方完成をして「平方根」の考え方で解いたりすることも可能ですが、因数分解で解くと一番素早く、そしてミスなく解くことができます。

テストなどで出題される二次方程式の問題では、因数分解を使うパターンがもっとも多いため、いろいろな問題にぜひ取り組んでください。

また、因数分解は式の構造を理解する助けにもなります。複雑に見える多項式も、因数分解によってシンプルな要素の積に分けると、式の成り立ちが見えやすくなります。これは数学のさまざまな場面で役立つ考え方で、高校以降の数学（例えば2次関数のグラフや最大最小問題など）でも頻繁に登場します。

因数分解は数学の基礎テクニックの一つであるため、苦手意識をなくせるように簡単な問題から少しずつ慣れていきましょう。

因数分解の基本的なやり方

因数分解にはいくつかの基本的なやり方があります。まず取り組むべきは共通の因数でくくる方法です。さらに、公式を使って因数分解する方法も重要です。公式に当てはまらない場合には特殊なテクニック（後述する「たすき掛け」など）を使うこともあります。

ここでは順を追って、基本的な因数分解のやり方を説明します。

共通項を使って因数分解する

もっとも基本的な因数分解の方法は、共通の項（共通因数）でくくることです。複数の項（たし算やひき算で繋がれた式の部分）に同じ因数が含まれている場合、その因数でくくる（くくる＝共通因数を前に出してかけ算の形にまとめる）ことができます。

例えば、式「3x – xy」を見てみましょう。2つの項 3xと -xy には、どちらにも x が含まれています。この x が共通因数です。そこで x で括ると、次のように因数分解できます。

3x - xy = x(3 - y)

また、項の数が3つ以上の場合も、すべての項に共通の因数があれば同様にくくりだせます。例えば「ax + ay + az」の場合、3項すべてに共通する因数である「a」くくることができるため、次のように因数分解できます。

ax+ay+az = a(x + y + z)

共通因数は数字の場合もあります。例えば「6x^2 + 9x」という式では、数の部分に共通因数 3、文字の部分に共通因数 x があります。両方をまとめてくくると次のように因数分解が可能です。

6x2 + 9x = 3x(2x + 3)

このようにまずは共通する数や文字がないかを探してくくり出すことで式を簡単にしましょう。

公式を使って因数分解する

共通因数でくくれない場合でも、特定の形に当てはまる式は因数分解の公式を利用できます。中学数学では覚えておくと便利な因数分解の公式がいくつかあります。式を見渡して、以下で紹介するパターン（公式の形）に当てはまっていないかをチェックすることで、スムーズに因数分解できる場合があります。

例えば、先ほど説明した「x2 + 5x + 6」で考えてみましょう。この式に一見共通因数はありませんが、この式は「x2 + (a+b )x + abという形をしています。先ほどまでの因数でくくる方法に合わせるのであれば、

x2 + 5x + 6 = x2 + 2x + 3x + 6

と考えることができ、これは 「(x2 + 2x) + (3x + 6)」に分けられます。それぞれで共通因数をくくると「x(x+2) + 3(x+2)」となり、さらに共通因数 (x+2) で括れば

x2 + 5x + 6 = (x2 + 2x) + (3x + 6) = x(x+2) + 3(x+2) = (x+2)(x+3)

と因数分解できました。このように、公式の形に当てはまると判断できれば、因数分解を一気に行うことができます。

したがって最終的な因数分解は次の通りです。

(x+2)(x+3)

因数分解の公式一覧

中学数学でよく使う因数分解の公式を4つ紹介します。因数分解をスムーズに行うためにぜひ覚えておきましょう！

(x+a)(x+b) の公式（一般的な2次式の因数分解）：
 x2 + (a+b)x + ab = (x+a)(x+b)
 例: x2 + 5x + 6 は 5を 2+3、6 を 2×3 と見て (x+2)(x+3)

完全平方の公式（(x+a)2）：
x2 + 2ax +  a2  = (x+a)2
例:x2 + 10x + 25 は 10x を 2×5×x、25 を 52 と見て (x+5)2。

完全平方の公式（(x-a)2）：
x2- 2ax +  a2 = (x-a)2
例: x2- 10x + 25 は -10x を -2×5×x、25 を 52 と見て (x-5)2。

差の平方の公式（2乗の差）：
x2- a2 = (x+a)(x-a)
例: x2 - 9 は 9 を 32 と見て (x+3)(x-3)。
また 4x2 - 49 のように係数がある場合は、一度 4x2-49 = (2x)2 - 72 とみなしてから (2x+7)(2x-7) の形にすると良いでしょう。

これら4つのパターンは頻出の因数分解です。式を見たときにすぐに「どの公式の形か」気付けるように、何度も練習してしっかり身につけましょう。

因数分解のテクニックを使った解き方

共通因数による因数分解や基本的な公式を使った因数分解に慣れたら、次はもう一歩進んだテクニックを身につけましょう。

ここからは応用編で、公式にあてはまらない因数分解の説明です。2次式や、文字が2種類以上含まれる式などは、一工夫が必要になります。中学生の範囲で役立つのは次の3つのテクニックです。

1. たすき掛け
2. 文字の置き換え
3. 次数の低い文字で整理する

それぞれの因数分解の手順を次の項で紹介します。

たすき掛けを使う

たすき掛け（たすきがけ）は、主に x2 の係数が1でない2次式（一般形「ax2+bx+c」）を因数分解する方法です。ちなみにこの方法は全国的に「たすき掛け」と呼ばれていますが、これは皆さんが知っている「襷（たすき）」が由来になっています。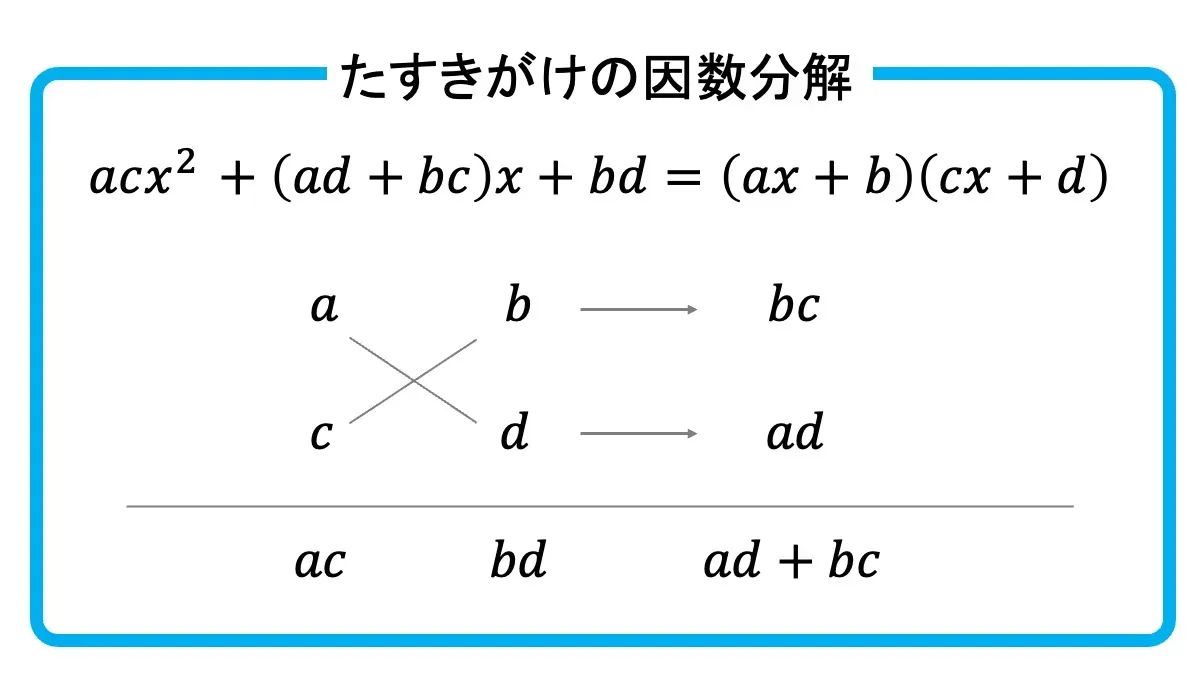

「襷」とは着物の袖をたくし上げてとめる帯のことで、斜めに交差させる形から、この方法が「たすき掛け」と呼ばれています。実際のたすきをイメージしながら、図や表を使って斜めに数を掛け合わせると、より分かりやすくなるでしょう。

まずは、「たすき掛け」を用いた因数分解の手順を簡潔に紹介します。

1. x2 の項の係数（a）を因数に分解する：かけ算をして「a」になる数の組み合わせ（因数のペア）をすべて考えます。
   例: 6x2 なら (1,6)、(2,3)（負の組み合わせも考えるなら (-1,-6)、(-2,-3)）。定数項（c）を因数に分解する：1と同様に、かけ算をして「c」になる数の組み合わせをすべて考えます。
   例: 8 なら (1,8)、(2,4)（負も含めれば (-1,-8)、(-2,-4)）。

2. 1.2で考えたそれぞれの組み合わせから、斜めに積を作って足し合わせることを考えます（これをたすき掛けの交差で表しています）。「ax2」の因数ペアを縦列に「c」の因数ペアを横列に置き、斜め同士を掛けて足したときに 「bx」（x の項）になる組み合わせを探します。

3. 組み合わせが見つかったら、その値を使って因数分解の形を書きます。一般に (ax2+bx+c) = ({一方の斜め積の元}x + {他方の斜め積の片方} )( {もう一方の斜め積の元}x + {斜め積のもう片方} ) の形に因数分解できます。

これが「たすき掛け」の手順です。少し抽象的で分かりにくいと感じた人も多いでしょう。ここからは「6x2 + 17x + 5」を例に用いて実際に因数分解をしながら説明します。

6x2  の因数ペアは (1,6) と (2,3)です。

定数5の因数ペアは (1,5)（「x」の係数が「17」で正であるため、負の因数のペアは必要ありません。）

これらを使って斜めに掛け算してみます。

(1,6) と (1,5) の組み合わせの場合、斜めの積は 1 × 5 = 5 と 6 × 1 = 6 になり、足すと 11 です。17にはなりません。次に (2,3) と (1,5) を試すと、斜めの積は 2 × 5 = 10 と 3 × 1 = 3 で、足すと 13 です。まだ17になりません。では、定数5の因数を逆に配置して (2,3) と (5,1)を試すと、斜め積が 2 × 1 = 2 と 3 × 5 = 15 となり、足すと 17 になります！これが bx の係数と一致しました。

組み合わせが見つかったので、このときの並べ方から因数分解の答えを出すと次のようになります。、

6x2 +17x+5 = (2x+5)(3x+1)

このようにたすき掛けを用いて因数分解をすることができました。 

たすき掛けのポイントは実際に紙に書き出して試すことです。複数の組み合わせを試行錯誤することになるため、最初はどうしても時間がかかりますが、慣れてくると効率よく見つけられるようになります。最初は失敗してもよいので、根気よく練習してみましょう。

文字に置き換える

次のテクニックは一時的に文字に置き換える方法です。複雑に見える式でも、一部を別の文字に置き換えることで公式が使いやすくなる場合があります。

例えば、式の中に共通して現れる部分を一文字で置き換えることで、計算を簡単にすることができます。

具体例を一つ挙げて考えてみましょう。

式「(a+b)2 + 6(a+b) + 9」を因数分解する方法を考えます。

このままだと複雑ですよね？そのようなときは、一時的に A = (a+b) と置き換えてみると、式がシンプルになります。

(a+b)2 + 6(a+b) + 9 = A2 + 6A + 9

これは公式「x2 + 2ax + a2」の形と同じです。

この式であれば、すぐに (A+3)2 と因数分解ができるでしょう。そしてここで、最後に置き換えた A を元の (a+b) に戻しましょう。

A2 + 6A + 9 = (A+3)2 =(a+b+3)2

これであっという間に因数分解の完成です！

このように、一見複雑に見える部分を別の記号に置き換えてシンプルな形にすると、因数分解すべき形が浮かび上がることがあります。置き換えたら必ず最後に元に戻すことだけは忘れずに、この考え方をぜひ活用してください

次数の低い文字で整理する

複数の文字を含む式（多変数の式）や、公式・たすき掛けではすぐに対応できない式の場合は、次数（べき乗の指数）の低い文字に注目して項を整理する方法が有効です。つまり、一方の文字について降べきの順（次数の高い順）に並べ直し、その文字でグループ分けして因数分解を試みます。

例えば、x と y 二つの文字を含む式x2+ 5xy + 2x + 10y を考えてみましょう。x は2乗の項がありますが、yにはありません。そのため、今回はyの次数に注目して項を並べ替えます。

y を含む項と含まない項でグループに分けると次のように整理ができます。

x2 + 5xy + 2x + 10y = (x2 + 2x) + (5xy + 10y)

前半はxに関する項、後半はyを含む項です。それぞれで共通因数をくくると、前半は x(x+2)、後半は 5y(x+2) となります。さらに共通因数 (x+2) が見つかるので、それでくくると最終的に因数分解された形は次のとおりです。

(x+2)(x+5y)

このように、次数の低い文字で整理してから因数分解することで、見通しが良くなり因数分解が成功しやすくなります。

もし整理した結果、因数が微妙に一致しない場合（例えば因数が (x-2) と (2-x) のように符号が逆になってしまった場合）でも慌てずに対処しましょう。

そのようなときは、2-x = -(x-2) のように符号を調整すれば、共通因数としてくくることができます。マイナス1でくくると因数の符号を反転できます。最終的に式全体の共通因数として同じ形にそろえてくくり出せれば、因数分解は成功です。

因数分解の練習問題

ここまで学んだ内容を確認するために因数分解の練習問題に挑戦してみましょう。基本的な問題から少し工夫が必要な問題まで4問を用意しました。まずは自分で解いて、下の解答と照らし合わせてください

因数分解の練習問題4問にチャレンジ！

1. 共通因数で括る問題： 8x3 + 4x2 を因数分解しましょう。

2. 公式を使う問題： x2 - 16 を因数分解しましょう。

3. たすき掛けを使う問題： 2x2+ 7x + 3 を因数分解しましょう。

4. 置き換え・工夫が必要な問題：x2 + 4xy + 3x + 12y を因数分解しましょう。

まずは各問題の式を見て、どの手法（共通因数、公式、たすき掛け、置き換え/整理）が使えそうか考えてください。

因数分解の練習問題4選の解答

1. 共通因数で括る問題の解答：
   8x3 + 4x2 は共通因数として 4x2 が含まれています。くくり出すと、4x2(2x + 1) となります。

2. 公式を使う問題の解答：
   x2 - 16 は 差の平方の公式に当てはまります。16 を 42 と見れば、(x+4)(x-4) と因数分解できます。

3. たすき掛けを使う問題の解答：
   2x2 + 7x + 3 を因数分解します。2x2の因数ペア (1、2)、定数3の因数ペア (1、3) を試すと、たすき掛けで 1 × 3 + 2 × 1 = 5（これは不一致）となります。入れ替えて 1 × 1 + 2 × 3 = 7（これは一致）です。よって、(x+1)(2x+3) と因数分解できます。

4. 置き換え・工夫が必要な問題の解答：
   x2 + 4xy + 3x + 12y は文字yに注目して整理します。(x2 + 3x) + (4xy + 12y) とグループ分けし、それぞれ因数分解すると x(x+3) + 4y(x+3) となります。共通因数 (x+3) をくくり出して、(x+3)(x+4y) と因数分解できます。

全部正解できた人、おめでとうございます。

もちろん、間違えた問題があっても大丈夫です。解答のプロセスを読み直して、どの方法を使えばよかったのかを確認しましょう。因数分解はパターンに気付くことと練習の積み重ねで上達します！

因数分解の解き方の流れ

最後に、因数分解の問題に直面したときの解き進め方を整理しておきましょう。一つの式を前にしたとき、次のポイントを順番に確認するとスムーズに因数分解の方針が立てられます。

共通因数でくくれるか確認

初めに、式のすべての項に共通する因数がないかを探します。同じ文字や同じ数字で割り切れる項ばかりなら、それが共通因数です。共通因数が見つかれば、真っ先にそれをくくり出して因数分解しましょう。

共通因数でくくるだけで因数分解が完了する場合もありますし、くくった後に残った式がさらに因数分解できる場合もあります。どちらにせよ、共通因数のチェックは因数分解の基本の一歩です。まずはこれを確認することから始めましょう！

公式を使えるか確認

共通因数でくくれないか、くくってもまだ複雑な形が残る場合は、因数分解の公式パターンに当てはまっていないかを確認します。

平方の和や差、一般形の2次式など、前述の4つの公式形に式が一致すれば、それを利用して一気に因数分解できます。具体的には「x2 の項があり、他に x の項と数字だけの項がある→(x+a)(x+b)の形かも？」「x2と数字だけの項で構成→差の平方かも？」などと試行錯誤してみましょう。

公式にハマる形だと気付けば解答まで一直線なので、くれぐれも見逃さないように！

置き換えが使えるか確認

共通因数や公式でも対処できないようなら、式を変形する工夫を考えます。特に x2 の係数が1以外の2次式では、たすき掛けができないか検討してみましょう。

また、式の中にひとまとまりになっている部分（例：(x+3) など）が繰り返し出てくるなら、その部分を一時的に別の文字に置き換えてシンプルにできないか考えます。そして、二つ以上の文字がある場合は、どの文字でグループ分けすると因数が見えそうかを探ります。一方の文字について降べきの順に並べ替えると、共通因数が浮かび上がることもあるでしょう。

上述の通り、公式に当てはまらない複雑な式は「たすき掛け」「置き換え」「項の並べ替え」によるグループ分けのいずれかを試してみましょう。最初は難しいかもしれませんが、練習するうちに「この形はあの方法が使えそうだな」とピンと来るようになります。そのように感覚が研ぎ澄まされるまで、ぜひ因数分解の演習を繰り返してください！

まとめ

ここまで、因数分解のやり方やテクニックについて紹介していきました。最後に、ポイントをおさらいしておきます。

• 式を積の形にまとめるのが因数分解
• 因数は式を作るもと
• 因数分解とは式をかけ算の形にすること
• 公式やたすき掛けを使って考える

そして、因数分解を簡単に進めるには以下の5つのポイントを意識しましょう：

• 4つの公式を使って考える
• xの係数に注目する
• 数字だけの項に注目する
• 数字だけの項の素因数分解をしてパターンを考える
• たすき掛けは書き出して試してみる

中学生のみなさんは、まずは基本のパターンをしっかり覚えて、たくさん問題を解いてみてください。最初は苦手でも、ポイントを押さえて練習を積めば因数分解はきっと得意になります。パズルを解くような感覚で楽しく因数分解に取り組んでみましょう！