【数学Ⅱ】三角関数をわかりやすく解説!図解でスッキリわかる入門講座

「三角関数の意味がわからない……」と悩んでいませんか?
「sin(サイン)」「cos(コサイン)」「tan(タンジェント)」といった言葉を聞いても、なんだか難しそうに感じてしまうかもしれません。しかし、決してそんなことはありません。
三角関数は、高校数学で最初につまずきやすい単元のひとつです。しかし定義やグラフのイメージをつかめれば理解しやすくなります。
この記事では、高校2年生のときに数学オリンピック本選に出場、学習塾に入らずに東大へ現役合格し、現在はカルぺ・ディエムでさまざまな講演活動を行っている永田耕作さん監修のもと、三角関数の意味・定義・公式を、図や具体例を使ってわかりやすく解説します。
永田先生
自分も、習ったばかりの頃はとにかく直角三角形や単位円を書いて、どう計算すればsin、cos、tanに求められるのか指でなぞりながら体に染み込ませました。
高校生になって初めて出てくる概念ですから、まずは定義を理解し、反射的に答えられるくらいまで頭にすり込むのがおすすめです!
編集部
塾選ジャーナル編集部
塾選ジャーナル編集部です。『塾選ジャーナル』は、日本最大級の塾検索サイト『塾選(ジュクセン)』が提供する、教育・受験に関する総合メディアです。保護者が知っておきたい受験や進路情報をお届けします。
監修者
永田耕作
2001年生まれ 東京大学教育学部卒 公立高校から学習塾に入らずに東大へ現役合格。中学・高校は野球部に所属、部活動と勉強を並行し 「練習で自分の苦手を潰して、試合で自分の力を最大限に発揮する準備をする」という努力の「型」を 勉強にも活かして受験勉強を乗り切る。得意科目は数学で、高校2年生のときに数学オリンピック本選に出場した経験がある。現在は(株)カルぺ・ディエムに所属し全国各地で年間100回以上の講演活動を行い、勉強モチベーションや計画の立て方などを伝えている。自著に、「東大生の考え型(2022,日本能率協会マネジメントセンター)」「東大式 数値化の強化書(2024,彩図社)」などがある。 X公式アカウント:https://twitter.com/nagatakosaku08

目次
三角関数とは?意味・定義を高校生向けにやさしく解説
三角関数とは、数学における「角度」と「長さ」の関係を表す関数です。
「なんとなく難しそう……」という印象を持つ人も多いですが、図形をイメージしながら考えることで分かりやすく解けます。
まずは三角関数の意味と定義について、やさしく丁寧に解説します。
三角関数とは三角比を拡張したもの
三角関数は、三角比の考え方をもっと広く、柔軟に使えるようにしたものです。
「90度より大きい角度でも値を定義したい」「大きい角度でも三角比を使えるようにして、実用的な計算をしたい」という関数として新たに定義されました。
その違いを理解するために、まずは三角比がどのようなものかを思い出してみましょう。
中学や高校1年生で学んだ三角比では、直角三角形の辺の比を使って「sin(サイン)」「cos(コサイン)」「tan(タンジェント)」を求めました。
例えば、次のような直角三角形を考えてみましょう。
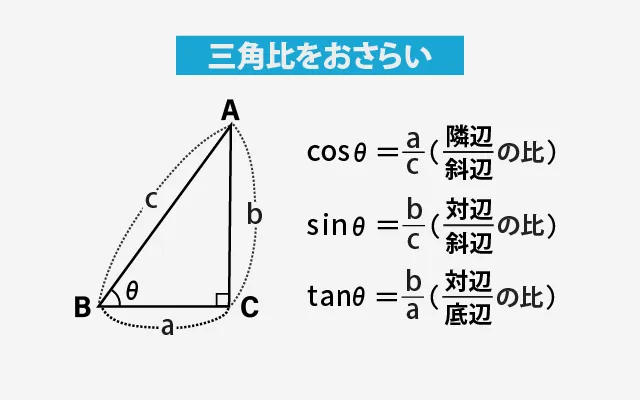
この図のように、
- sinθ = 対辺 ÷ 斜辺(b/c)
- cosθ = 隣辺 ÷ 斜辺(a/c)
- tanθ = 対辺 ÷ 隣辺(b/a)
と定義されていました。
しかしここでひとつ疑問が出てきます。「角度が90度より大きいときはどうするの?」という問題です。
直角三角形では、扱える角度は0度より大きく90度未満までです。しかし高校数学では、180度やそれ以上の角度に対しても sin や cos を使う必要が出てきます。
この問題を解決するのが、「単位円(たんいえん)」による定義です。
単位円を使うことで、どんな角度でも三角関数の値を定義できるようになります。
sin・cos・tanの意味
三角関数では、sin・cos・tanの3つが基本となります。
それぞれは「角度と辺の比」を表し、直角三角形では以下のように定義されます。
sin=「対辺 ÷ 斜辺」
- θに対してどれだけ上に伸びているかを示す比です。
- 0°~90°以下の範囲であれば角度が大きくなるほど、sinθも大きくなり、最大値は1です。
cos=「隣辺 ÷ 斜辺」
- θに対してどれだけ横に伸びているかを示す比です。
- 0°~90°以下の範囲であれば、角度が大きくなるほどcosθの値は小さくなります。
tan=「対辺 ÷ 隣辺」
- 縦と横の比を表します。
- 図で見ると、θの角度によって急な坂か、ゆるやかな坂かを表すイメージです。
- 角度が0度から90度に近づくと、tanθの値は急激に大きくなり、無限にちかづきます。
永田先生
三角関数は、実は数学だけでなく、他の分野でも使われています。
例えば、物理では斜面を転がる物体の運動で、重力が斜面に沿ってどれくらいかかるかを計算するときや振り子の運動で時間と共に変化する角度を表すときなどにsinやcosを使います。
建築分野では、屋根の角度や長さの計算にtanをはじめとする三角関数を用いたり、建物がどれくらい日光を取り入れられるかを、三角関数を使って計算したりするようです。
「三角関数を習っても意味あるの?」と考える方もいらっしゃるかもしれませんが、生活やほかの学問にも応用されているんですよ!
単位円で覚える三角関数のイメージ
三角関数をより深く理解するには、「単位円」という考え方がとても重要です。
三角比では直角三角形が前提でしたが、それだけでは90度より大きな角度や負の角度を扱うことができません。
単位円を使えば、cosθが0になってしまう角度(90°や270°など)を除き、すべての角度に対してsin・cos・tanの値を定義できるようになります。
ここでは、「単位円とは何か」「なぜ必要なのか」について、イラストを交えてわかりやすく解説します。
単位円とは?なぜ必要なの?
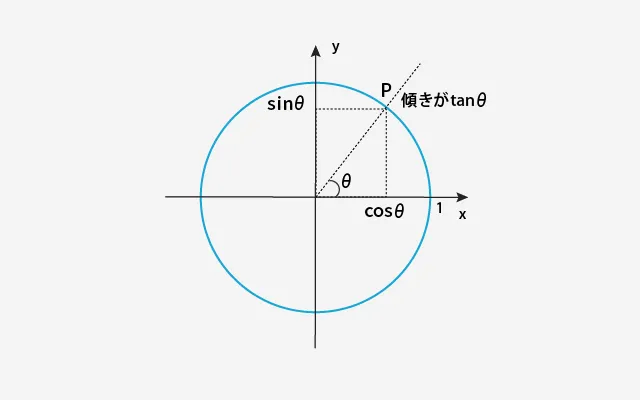
単位円とは、半径が1の円のことです。図のように、中心を原点(0,0)とした円を使って、角度と座標の関係を見るのがポイントです。

単位円では、角度θに対応する点Pのx座標がcosθ、y座標がsinθになります。
これによって、
- 0〜90度の角度(第1象限)
- 90〜180度(第2象限)
- 180〜270度(第3象限)
- 270〜360度(第4象限)
のすべての範囲でsinとcosの符号と値を把握できるようになります。
角度と座標の関係を覚えよう
単位円では、角度を「円周上の点の位置」として表現できます。そしてその点の座標(x, y)が、三角関数のcosθとsinθの値になるという仕組みです。
原点を中心とした単位円で、半径1の長さをもつ点Pを考えましょう。この点Pが作る角度をθ(反時計回り)としたとき、点Pの座標は次のようになります。

このように、cosθ = 点Pのx座標(横の長さ)、sinθ = 点Pのy座標(縦の長さ)と定義されているのです。
角度θを回転させていくと、点Pの位置も変わります。すると当然、x座標(cosθ)やy座標(sinθ)も変化します。
すなわち、以下のような関係が成り立ちます。
- θ=0° → 点Pは (1, 0) ⇒ cos0°=1, sin0°=0
- θ=90° → 点Pは (0, 1) ⇒ cos90°=0, sin90°=1
- θ=180° → 点Pは (−1, 0) ⇒ cos180°=−1, sin180°=0
なお、tanθも単位円で定義できます。実は、tanθ = sinθ ÷ cosθという性質を使って、cosθ ≠ 0 の範囲で値が決まるのです。
ただし、cosθが0になる90°や270°などではtanθは「定義できない(∞に発散)」点にも注意が必要です。
永田先生
この単位円を使えば、θに対する三角関数の値が簡単に求められます。まず、図のように単位円上の点P(x, y)について、x軸上の正方向とOPのなす角をθとします。
sinθ=y/1=y
cosθ=x/1=x
tanθ=y/x
これまでの定義通り三角関数を計算すると、単位円の半径を踏まえて斜辺の長さが1であるためsinとcosはそれぞれ点Pのy座標、x座標に等しくなるのです。また、tanはOPの傾きと一致します。
単位円でなくても、定義通り計算すれば三角関数の値を求めることが可能ですが、半径1の単位円を使うことで、値をより計算しやすくしているのです。
グラフで覚えよう!三角関数の特徴
三角関数の理解を深めるためには、「グラフの形」をしっかりイメージすることがとても大切です。
特に sinと cosは、定期テストでもよく出題される重要ポイントです。
ここでは、sinとcosのグラフ形と特徴を、図解とともにやさしく解説します。
sin・cosのグラフの形と特徴
まずはsinθのグラフから見ていきましょう。y=sinθのグラフは、波のように上下に揺れるカーブです。
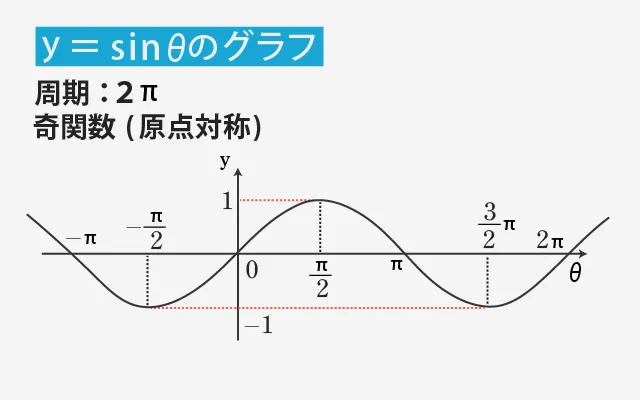
θ=0のときにsinθ=0からスタートし、
- θ=90°(π/2)でsinθ=1(最大値)
- θ=180°(π)でsinθ=0に戻る
- θ=270°(3π/2)でsinθ=−1(最小値)
- θ=360°(2π)で再び0に戻ります
これがsinθの1周期(2π)です。
この波形は、角度が増えるたびに繰り返されていくのが特徴です。
y=cosθも、y=sinθと同じような波の形をしていますが、スタート位置が違う点に注意しましょう。
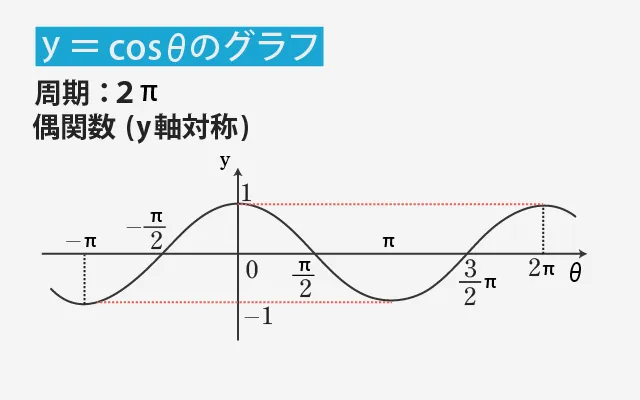
cosθは、θ=0のときに1から始まり、
- θ=90°で0、
- θ=180°で−1、
- θ=270°で0、
- θ=360°で1に戻ります。
cosθのグラフはsinθのグラフを左に90°(π/2)ずらしたものになっています。
永田先生
それぞれのグラフの形を忘れないために、いくつか抑えるポイントがあります。
まずは大まかに、この上下に波打つ波形を覚えておきましょう。そして、sin波の場合は原点を通ること、cos波の場合は点(0,1)を通ることを抑えてください。これはsinxとcosxのxにそれぞれ0を代入すればすぐにわかります。
さらに、周期については、単位円を想像してみて、動径(単位円上を動く点と単位円の中心を結ぶ半径)がx軸に重なるのは360度(2π)ごとだと思い出すことができれば、周期もすぐに分かるでしょう。
tanのグラフのクセと注意点
tan)のグラフは、sinやcosとは大きく異なる特徴を持っています。
sinやcosのように波のように上下にゆらぐ動きとは違い、tanは無限に近づく動きを繰り返すグラフです。
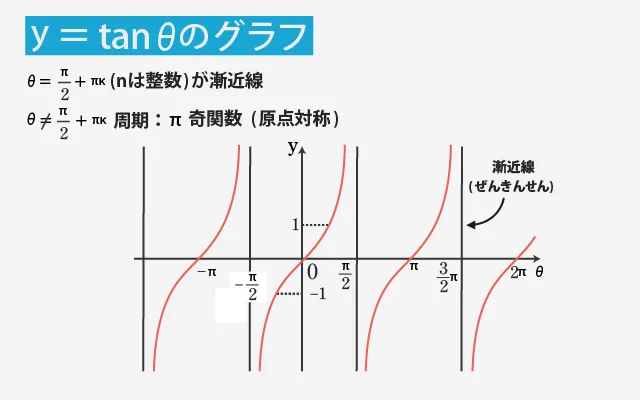
tanθは、sinθ ÷ cosθ で定義される三角関数です。
この性質から、cosθ=0となる角度(90°や270°など)では、tanθは定義できません。
つまり、グラフ上ではその角度の直前・直後で、急激に値が発散(∞に向かう)することになります。
tanθのグラフの特徴として、以下のポイントを押さえておきましょう。
- 周期はπ(180°):sinやcosより短い!
- y軸方向に無限に発散する場所がある(cosθ=0のとき)
- 連続的に波打つグラフではなく、「切れ目」があるのが特徴
- θ=0°ではtanθ=0からスタートし、右肩上がりに増加していく
- 90°や270°などでcosが0になるため、その位置に漸近線(垂直線)が入る
三角関数で絶対覚えておきたい公式
三角関数には、テストや入試で問われる重要な公式が多数存在します。
ここでは、覚えておきたい三角関数の代表的な恒等式と、それが持つ意味・使いどころを解説します。
永田先生
三角関数の公式は、複雑な三角関数に関する計算をシンプルにしたり、波や振動のような現象を数式で正確に表したりするためにあります。計算を簡単にするのは、ミスを減らすために重要なので、公式の導出を理解したうえでしっかり頭に入れ、さらに使いこなせるようにしておきましょう。
とはいえ、すべての公式を丸暗記する必要はありません。加法定理を覚えていれば、2倍角や半角の公式、和積・積和の公式を導出できるし、対称性の公式は単位円が頭に入っていれば自然と導けます。必要な部分をしっかり暗記し、導出可能なものは導出方法を覚えておくことが大事です。
三角関数の相互関係と対称性に関する公式
三角関数の相互関係に関する公式
三角関数には、sin・cos・tanを相互に関連づける重要な公式があります。特に以下の3つは頻出で、必ず押さえておきたい内容です。
- tanθ = sinθ ÷ cosθ:タンジェントは、サインとコサインの比で表せます。三角方程式の解法やグラフ解析で頻繁に使われる基本公式です。
- sin²θ + cos²θ = 1:単位円に基づく基本恒等式で、式の変形や代入、置き換えに頻繁に登場します。
- 1 + tan²θ = 1 ÷ cos²θ:タンジェントとコサインの関係を表す式です。
三角関数の対称性に関する公式
また、三角関数には、角度を正負にしたときや、180°をはさんだときに値がどう変化するかという「対称性」の性質があります。
- sin(−θ) = −sinθ
- tan(−θ) = −tanθ
- cos(−θ) = cosθ
さらに重要なのが、180°を基準にした角度変換のパターンです。これらは第2象限・第3象限での符号変化やグラフ形状を予測する際に役立ちます。
- sin(180°−θ) = sinθ
- cos(180°−θ) = −cosθ
- tan(180°−θ) = −tanθ
これらの式は、角度の変形や三角方程式の解法でも非常によく使われるので、反復練習で自然に使えるようにしておきましょう。
加法定理とその応用に関する公式
三角関数には、「角度の和・差」に対応する計算式があり、これを加法定理と呼びます。
さらに、そこから派生する2倍角・半角・3倍角の公式、そして和積・積和の公式なども頻出です。
どれも式の変形や三角方程式、波の合成などに使われる重要な公式です。順を追ってわかりやすく紹介していきます。
基本の加法定理
加法定理は、2つの角の和・差に対する三角関数の値を求める公式です。式の中に「A」と「B」のような複数の角度がある場合に大活躍します。
| 加法定理(和と差) | |
|---|---|
| sin(A±B) | sinA·cosB ± cosA·sinB |
| cos(A±B) | cosA·cosB ∓ sinA·sinB |
| tan(A±B) | (tanA ± tanB) ÷ (1 ∓ tanA·tanB) |
2倍角の公式(sin2θ, cos2θ, tan2θ)
加法定理を使えば、θ + θ = 2θ の場合の式(=2倍角公式)も導出できます。
| 2倍角の公式(主要形) | |
|---|---|
| sin2θ | 2sinθ·cosθ |
| cos2θ | cos²θ − sin²θ
= 2cos²θ − 1 = 1 − 2sin²θ |
| tan2θ | (2tanθ) ÷ (1 − tan²θ) |
半角の公式(θ/2)
2倍角を逆向きに使うことで、半角の公式も導き出せます。特徴として、平方根や ±(符号の判定)が入ることに注意しましょう。
| 半角の公式(主要形) | |
|---|---|
| sin²(θ/2) | (1 − cosθ) / 2 |
| cos²(θ/2) | (1 + cosθ) / 2 |
| tan²(θ/2) | (1 − cosθ) / (1 + cosθ) |
3倍角の公式(sin3θ, cos3θ, tan3θ)
3倍角の公式は、加法定理+2倍角を組み合わせた拡張公式です。
| 3倍角の公式 | |
|---|---|
| sin3θ | 3sinθ − 4sin³θ |
| cos3θ | 4cos³θ − 3cosθ |
| tan3θ | (3tanθ − tan³θ) ÷ (1 − 3tan²θ) |
和積の公式(和→積)
和積公式は、2つの三角関数の和・差を積に変換する公式です。
積に変えることで、式を簡潔にし、積分や変形で扱いやすくなります。
| 和積の公式(和→積) | |
|---|---|
| sinA + sinB | 2sin((A+B)/2)·cos((A−B)/2) |
| sinA − sinB | 2cos((A+B)/2)·sin((A−B)/2) |
| cosA + cosB | 2cos((A+B)/2)·cos((A−B)/2) |
| cosA − cosB | −2sin((A+B)/2)·sin((A−B)/2) |
積和の公式(積→和)
逆に、積和公式は、三角関数の積を和に変換する公式です。
| 和積の公式(和→積) | |
|---|---|
| sinA·sinB | {cos(A−B) − cos(A+B)}/2 |
| cosA·cosB | {cos(A−B) + cos(A+B)}/2 |
| sinA·cosB | {sin(A+B) + sin(A−B)}/2 |
三角関数の合成公式
三角関数の合成公式は、sinとcosの和を1つの三角関数にまとめるテクニックです。
この公式を使うと、sinθ + cosθなどの式を、単一のsin関数として表すことができ、計算や解析がシンプルになります。
a·sinθ + b·cosθ の形の式は、以下のように1つのsin関数にまとめらます。
a·sinθ + b·cosθ = √(a² + b²)·sin(θ + α)
ここで、α は角度で、tanα = b / a という関係であることに注意しておきましょう。具体的には、sinθ + cosθ の和を、この公式を使ってひとつの sin 関数に変換できます。
定期テスト対策!三角関数のよく出る問題
三角関数のテストでは、公式の使い方や計算の流れが問われることが多いです。
ここでは、練習問題を用いて、公式の使い方をマスターしておきましょう。
三角比の相互関係と周期性に関する公式の問題
Q1.角度θが第1象限にあるとき、sinθ = 3/5 の場合、cosθ の値を求めなさい。
Q2.角度θが第2象限にあるとき、cos(180° − θ) = −cosθ を利用して、θが120°の場合のcos(180° − θ)の値を求めなさい。
加法定理とその応用に関する公式の問題
Q3.角度A = 30°、B = 45°のとき、次の式の値を求めなさい。
sin(30° + 45°)
Q4.角度θ = 60°のとき、cos2θの値を求めなさい。
三角関数の合成公式の問題
Q5.sinθ + cosθ を合成公式を用いて、単一の sin 関数の形に変形しなさい。
定期テスト対策!三角関数のよく出る問題【解説編】
三角比の相互関係と周期性に関する公式の問題の解説
Q1.角度θが第1象限にあるとき、sinθ = 3/5 の場合、cosθ の値を求めなさい。
解法のステップ
- sin²θ + cos²θ = 1 という恒等式を利用します。
- sinθ = 3/5 なので、sin²θ = (3/5)² = 9/25 です。
- この値を恒等式に代入して、cos²θを求めます。
- cos²θを求めたら、cosθの値を計算します。
解答の流れ
- sin²θ = (3/5)² = 9/25
- 1 − sin²θ = cos²θ
- 1 − 9/25 = cos²θ
- 25/25 − 9/25 = cos²θ
- 16/25 = cos²θ
- cosθ = √(16/25)
- cosθ = 4/5
Q2.角度θが第2象限にあるとき、cos(180° − θ) = −cosθ を利用して、θが120°の場合のcos(180° − θ)の値を求めなさい。
解法のステップ
- 公式 cos(180° − θ) = −cosθ をそのまま使います。
- 角度 θ = 120° を代入します。
- cos(120°) を求め、公式に代入して結果を出します。
解答の流れ
- cos(180° − 120°) = −cos(120°)
- cos(180° − 120°) = −(−1/2)
- cos(60°) = 1/2
- よって、cos(180° − 120°) = 1/2
加法定理とその応用に関する公式の問題の解説
Q3.角度A = 30°、B = 45°のとき、次の式の値を求めなさい。
sin(30° + 45°)
解法のステップ
- sin(A + B) の加法定理を使います。
- sin(A + B) = sinA cosB + cosA sinB を使って、角度A = 30°、B = 45°を代入します。
- 各三角関数の値を求めて計算します。
解答の流れ
- sin(30° + 45°) = sin30° cos45° + cos30° sin45°
- sin30° = 1/2, cos30° = √3/2, sin45° = √2/2, cos45° = √2/2
- sin(30° + 45°) = (1/2) * (√2/2) + (√3/2) * (√2/2)
- = (√2/4) + (√6/4)
- = (√2 + √6) / 4
Q4.角度θ = 60°のとき、cos2θの値を求めなさい。
解法のステップ
- cos2θ の公式を使います。
- 2倍角の公式には複数の形がありますが、ここでは cos2θ = cos²θ − sin²θ を使います。
- 角度θ = 60°の値を代入して計算します。
解答の流れ
- cos2θ = cos²θ − sin²θ
- cos(60°) = 1/2, sin(60°) = √3/2
- cos2(60°) = (1/2)² − (√3/2)²
- = 1/4 − 3/4
- = −2/4
- = −1/2
三角関数の合成公式の問題の解説
Q5.sinθ + cosθ を合成公式を用いて、単一の sin 関数の形に変形しなさい。
解法のステップ
- 合成公式を使います。
合成公式は以下の形で表されます:
a·sinθ + b·cosθ = √(a² + b²)·sin(θ + α)
ここで、a=1、 b=1とします。 - a² + b² の計算
√(a² + b²)= √2 - α を求める
tanα = b / a なので、
tanα=1/1=1
これから α = π/4 となります。 - 変形後の式
したがって、sinθ+cosθ=√2sin(θ + π/4)となります。
三角関数についてよくある質問(FAQ)

三角関数は高校数学で避けて通れない重要な分野です。ここでは、よく寄せられる質問とその答えをわかりやすく紹介します。
三角関数で覚えておくべき比はありますか?
以下の三角関数の値は、三角形の基本的な角度に対応するもので、覚えておくとテストや実際の問題で大いに役立ちます。
| 角度 | sin(θ) | cos(θ) | tan(θ) |
|---|---|---|---|
| 30° | 1/2 | √3/2 | 1/√3 |
| 45° | √2/2 | √2/2 | 1 |
| 60° | √3/2 | 1/2 | √3 |
加えて、次の特別な角度(0°、90°、180°)の三角比も覚えておきましょう。
| 角度 | sin(θ) | cos(θ) | tan(θ) |
|---|---|---|---|
| 0° | 0 | 1 | 0 |
| 90° | 1 | 0 | 定義なし |
| 180° | 0 | −1 | 0 |
三角関数のsin、cos、tanってどこのことですか?
三角関数では、sin・cos・tanの3つが基本となります。
それぞれは「角度と辺の比」を表すもので、具体的には以下のように定義されます。
sin=「高さ ÷ 斜辺」
- θに対してどれだけ上に伸びているかを示す比です。
- 角度が大きくなるほど、sinθも大きくなります(最大値は1)。
cos=「底辺 ÷ 斜辺」
- θに対してどれだけ横に伸びているかを示す比です。
- 角度が大きくなるにつれて、cosθの値は小さくなっていきます。
tan=「高さ ÷ 底辺」
- 縦と横の比を表します。
- 図で見ると、θの角度によって急な坂か、ゆるやかな坂を表すイメージです。
- 角度が90度に近づくと、tanθの値は急激に大きくなります(無限に発散)。
三角関数は高校何年生で習いますか?
三角関数は、主に高校1年生の後半から2年生で学びます。
高校での数学のカリキュラムにおいて、三角関数は重要な位置を占めており、特に以下のタイミングで学習します。
高校1年生(後半):数学I
三角比の基本(sin、cos、tan):高校1年生の後半、直角三角形における三角比として、sin、cos、tanを最初に学びます。
この時期には、三角形の辺の比や三角比の計算方法が登場します。
三角関数の基礎: 同じく1年生の後半には、三角比を拡張した三角関数(sin、cos、tanの一般的な定義)を学び、単位円を使って、どの角度でも三角関数の値を求める方法を習います。
高校2年生:数Ⅱ
三角関数の応用:高校2年生では、三角関数の加法定理や合成公式、三角方程式など、少し難しい内容に進みます。また、三角関数のグラフや、周期性、最大値・最小値の計算などが登場するのが特徴です。
数学は塾に通って対策すべきですか?
数学が苦手だと感じている方には、塾のサポートを活用することをおすすめします。数学が苦手と言っても、つまずいている箇所や課題は人それぞれ異なります。自分に合った学習方法を見つけることが大切です。
数学が苦手という理由で、「何から始めていいかわからない」という方も多いでしょう。
塾に通うことで、つまずいている箇所をピンポイントで解決したり、理解が深まるまで繰り返し学習したりすることができます。
数学に強い塾について詳しく知りたいという方は、以下の記事をご覧ください。
まとめ 三角関数は定義に立ち返って解こう!
三角関数を解くためには、その定義をしっかり理解することが最も大切です。
まず、sin、cos、tanの基本的な意味を覚えておくと、問題がスムーズに解けます。基本的な公式も、定義に立ち返れば理解がやさしくなります。また、三角関数のグラフや周期性を意識することも重要です。
問題を解く際には、公式を使いこなし、グラフの特徴を理解することが重要です。これで、テストや応用問題でも自信を持って取り組むことができます。
焦らずに、基本をしっかり押さえれば、必ず理解が深まります。自信を持って進んでいきましょう!
執筆者プロフィール

塾選ジャーナル編集部です。『塾選ジャーナル』は、日本最大級の塾検索サイト『塾選(ジュクセン)』が提供する、教育・受験に関する総合メディアです。保護者が知っておきたい受験や進路情報をお届けします。
監修者プロフィール

2001年生まれ 東京大学教育学部卒 公立高校から学習塾に入らずに東大へ現役合格。中学・高校は野球部に所属、部活動と勉強を並行し 「練習で自分の苦手を潰して、試合で自分の力を最大限に発揮する準備をする」という努力の「型」を 勉強にも活かして受験勉強を乗り切る。得意科目は数学で、高校2年生のときに数学オリンピック本選に出場した経験がある。現在は(株)カルぺ・ディエムに所属し全国各地で年間100回以上の講演活動を行い、勉強モチベーションや計画の立て方などを伝えている。自著に、「東大生の考え型(2022,日本能率協会マネジメントセンター)」「東大式 数値化の強化書(2024,彩図社)」などがある。 X公式アカウント:https://twitter.com/nagatakosaku08












