【中学3年】三平方の定理（ピタゴラスの定理）とは？5分で理解できる公式と証明の解説

三平方の定理とは？

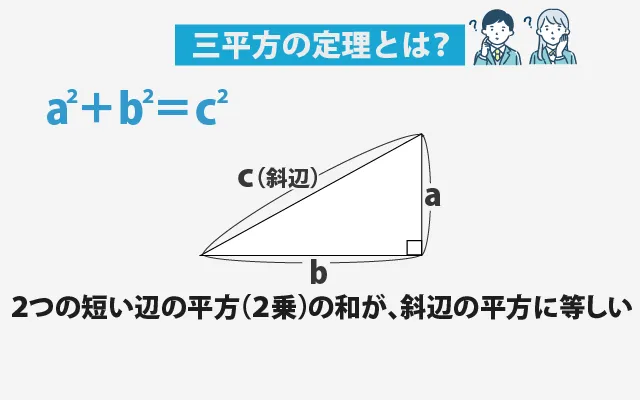
三平方の定理（ピタゴラスの定理）とは、直角三角形の3つの辺の長さに関するきまりのことです。この定理を使うと、2つの辺の長さがわかっているときに、もう1つの辺の長さを求めることができます。

例えば、少し離れた地面から建物の屋上までの距離や坂道の長さなど、「ななめの距離」を知りたいときに役立つ考え方です。数学の中では、直角三角形に必ず成り立つルールとして非常に重要な定理です。

この定理は、古代ギリシャの数学者「ピタゴラス」にちなんで「ピタゴラスの定理」とも呼ばれています。日本では「三平方の定理」という名前で教科書に登場します。

直角三角形の3つの辺には特別な関係がある

直角三角形には、3つの辺の長さの間に特別な関係があります。直角をはさんでいる2つの辺を「a」と「b」、直角の向かいにある一番長い辺を「c（斜辺）」とすると、次のような関係が成り立ちます。

a² ＋ b² ＝ c²

この式は、「2つの短い辺の平方（2乗）の和が、斜辺の平方に等しい」という意味です。 つまり、直角三角形では3つの辺が常にこの関係を満たしています。

このきまりを三平方の定理（ピタゴラスの定理）と呼びます。どんな直角三角形でも、3つの辺の長さがこの関係で結ばれていることがわかるのです。

公式は a²＋b²＝c²

三平方の定理を数式で表すと、次のようになります。

a² ＋ b² ＝ c²

この式は、「直角をはさんでいる2辺の平方（2乗）の和が、斜辺の平方に等しい」という意味です。ここでいう「平方（へいほう）」とは、同じ数を2回かけることを表します。たとえば、3の平方は「3×3＝9」、4の平方は「4×4＝16」です。

つまり、次のような関係になります。

もし a＝3、b＝4 のとき、
a²＋b²＝3²＋4²＝9＋16＝25 となり、
c²＝25 → c＝5 となります。（辺の長さは正の値であるため）

このように、2つの辺の長さがわかれば、残りの1辺（斜辺やほかの辺）を求めることができるのが三平方の定理の大きな特徴です。

三平方の定理をかんたんに証明【5分でマスター！】

三平方の定理（ピタゴラスの定理）は、面積の考え方を使うと、図形的にわかりやすく証明できます。ここでは、「正方形を使った証明」という最も基本的な方法を紹介します。

この証明は、直角三角形を4つ使って1つの大きな正方形を作る考え方です。実際に図を見ながら確認すると、三平方の定理が自然に導かれることがわかります。

ステップ1 正方形を使って考えてみる

三平方の定理は、正方形を使って面積の関係を考えると、むずかしい計算をしなくても納得できます。

まず、一辺の長さが a＋b の大きな正方形を考えます。その中に、同じ大きさの直角三角形を4つ入れてみましょう。4つの三角形を角を合わせるように並べると、中央に小さな正方形ができます。

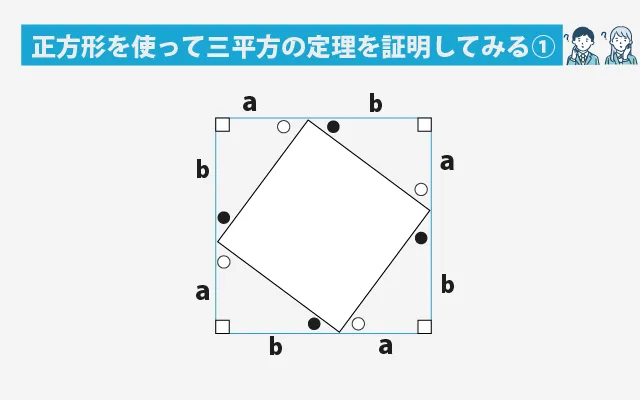
このとき、中央の小さな正方形の一辺の長さは「c（斜辺）」になります。つまり、大きな正方形の中には「4つの三角形」と「1つの小さい正方形」が入っていることになります。

この図を使うと、直角三角形の3つの辺（a、b、c）の面積の関係を見つけることができるのです。

ステップ2 面積の関係から導く

先ほどの図には、「大きな正方形」と「4つの直角三角形」、そして「中央の小さな正方形」がありました。このとき、それぞれの面積の関係を比べることで、三平方の定理を確かめることができます。

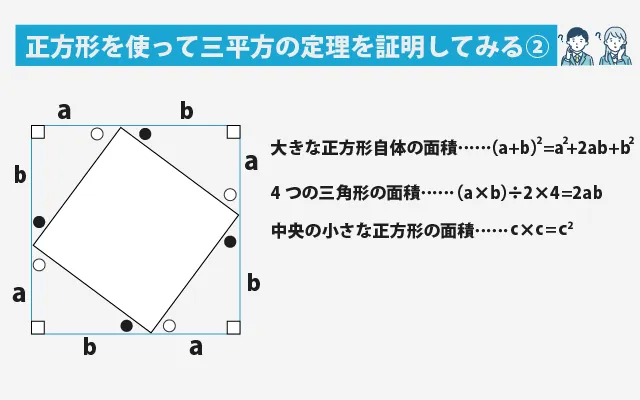
まず、大きな正方形自体の面積は、 (a＋b)² = a²＋2ab＋b² となります。縦×横ですね。

次に、4つの三角形と中央の小さな正方形を合わせた面積を考えます。直角三角形1つの面積は (a×b)÷2 なので、4つで 2ab。それに中央の小さな正方形の面積 c² を足すと、c²＋2abとなります。

これら2つの面積は同じ正方形を表しているため、a²＋2ab＋b² = c²＋2abが成り立ちます。

両辺の「2ab」を引くと、次の関係式が残ります。a²＋b²＝c²

このようにして、図形の面積のつり合いから三平方の定理を導くことができます。

三平方の定理でおさえたいポイント

三平方の定理を学ぶときに、特に意識しておきたい基本のポイントを整理しておきましょう。これらを理解しておくと、問題を解くときに迷わずに公式を使えるようになります。

斜辺の位置を確認しよう

三平方の定理では、斜辺（しゃへん）の位置を正しく理解することがとても大切です。直角三角形では、直角の向かい側にある一番長い辺が斜辺になります。

たとえば、次のような直角三角形を考えてみましょう。

直角をはさんでいる2つの辺を「a」と「b」、直角の向かい側の長い辺を「c」とすると、この「c」が斜辺になります。

この関係をもとに、三平方の定理の公式
a²＋b²＝c²
が成り立ちます。

もし斜辺の位置を間違えてしまうと、公式を正しく使っても答えが合わなくなることがあります。計算を始める前に、どの辺が斜辺なのかを必ず図で確認しましょう。

公式の位置関係を間違えない

三平方の定理の公式は、次のように書きます。

a²＋b²＝c²

このとき、右側（＝の右側）にくる「c²」が斜辺の2乗です。つまり、「直角の向かい側の辺（斜辺）」は、基本的に式の右側に書きます。

たとえば、直角三角形の辺の長さを a＝3、b＝4、c＝5 とすると、
3²＋4²＝5²
9＋16＝25
のように計算が成り立ちます。

もし公式の左右を逆にしてしまうと、 「どの辺がどの記号にあたるのか」がわからなくなり、計算を間違えやすくなります。慣れてきたら変えてもいいですが、慣れるまでは順番を決めておくといいでしょう。

特殊な三角形について確認

三平方の定理では、整数の長さできれいに成り立つ三角形があります。これを知っておくと、計算しなくてもすぐに答えを出せる場合があります。

もっとも有名なのが「3・4・5の三角形」です。これは次のような関係が成り立ちます。

3²＋4²＝5²
9＋16＝25

つまり、3cm・4cm・5cm の直角三角形では、三平方の定理の公式 a²＋b²＝c² がぴったり成り立つ<のです。

このような三角形は「整数比できれいに計算できる」ため、定期テストや入試の図形問題でもよく登場します。

ピタゴラス数を覚えておく

三平方の定理を満たす整数の組み合わせを、ピタゴラス数（またはピタゴラスの数）といいます。これらは、直角三角形の3つの辺の長さとして使うことができる便利な数の組です。

もっとも基本的なピタゴラス数は「3・4・5」です。このとき、次の関係が成り立ちます。

3²＋4²＝5²
9＋16＝25

つまり、3cm・4cm・5cm の三角形は直角三角形になります。このような組み合わせはほかにもあります。

5・12・13

8・15・17

これらも、a²＋b²＝c² の関係を満たしています。

ただし、最初の段階では「3・4・5」だけを確実に覚えておけば十分です。この組み合わせは最もよく使われ、テストでも頻出です。

三平方の定理を例題で確認しよう

ここまで学んだ三平方の定理を、実際の計算で確かめてみましょう。例題を通して、公式 a²＋b²＝c² の使い方を確認します。

例題

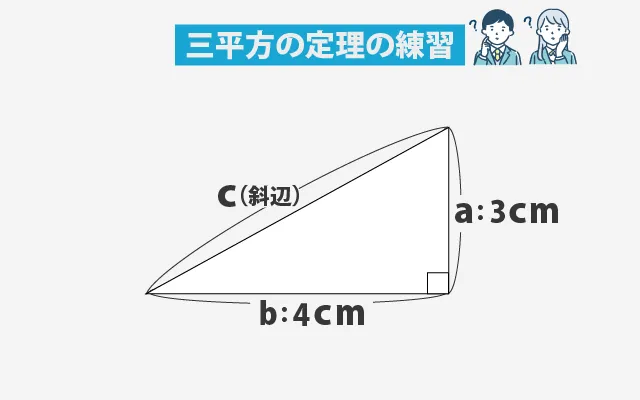
短い2つの辺が3cmと4cmの直角三角形があります。このとき、斜辺の長さ c を求めましょう。

解き方の手順

① まず、三平方の定理の公式を使います。
a²＋b²＝c²

② a＝3、b＝4 を代入します。
3²＋4²＝c²

③ 計算します。
9＋16＝c²
25＝c²

④ c を求めます。
c＝√25（cは辺の長さで、正の数であるため）
c＝5

答え

斜辺の長さは5cmになります。

まとめ 三平方の定理の基本を整理しよう

三平方の定理（ピタゴラスの定理）は、直角三角形の3つの辺の長さに成り立つ関係を表した重要な定理です。直角をはさんでいる2辺をa・b、直角の向かいにある一番長い辺（斜辺）をcとすると、次の公式が成り立ちます。

a²＋b²＝c²

この関係は、どんな直角三角形でも必ず成り立ちます。

三平方の定理は、図形問題の基礎になる考え方です。まずはこの公式をしっかり覚えて、「どの辺がa・b・cにあたるのか」を図で確認する習慣をつけましょう。これができれば、次の段階（高さ・距離・立体の応用）もスムーズに理解できます。