中学数学の二次方程式の解き方！解法3パターンをわかりやすく解説

本記事では中学数学における二次方程式の解き方について解説をしていきます。二次方程式の代表的な解法3パターンから複雑な二次方程式の解き方まで練習問題を使って分かりやすく解説をしています。二次方程式が分からなくてお困りの方はぜひこの記事を参考にしてみてください。

「二次方程式の解き方がわからない」 「解の公式は覚えたけれど、使い方がわからない」

数学の勉強を頑張っているけれど、二次方程式が解けなくて悩んでいる人も多いのではないでしょうか？

さっそくですが、二次方程式の解き方の基本は以下の3つです。

二次方程式の解き方の基本

二次方程式の問題は上記の3つの基本的な解き方を身につけ、素早く正確に解けるようになるまで練習を繰り返しましょう。 二次方程式は、文章題や関数の問題、三平方の問題などでも利用することが多いからです。

また解の公式を使ってすべての二次方程式を解こうとする中学生が多いのですが、実はそれはあまり効率的な方法ではありません。 それよりも、平方根を使った考え方と因数分解を使った考え方をしっかり身につけ、状況に合わせて適切な解き方を選択することが重要です。

この記事でわかるポイント

本記事では、二次方程式の解き方や練習の仕方、さらには中学数学全般の成績を上げるための効率のよい勉強法について解説します。 練習問題も掲載していますので、素早く正確に解けるようになるまで練習してくださいね。

1.二次方程式の解き方

二次方程式を解くためには、基本的な解法をしっかりと理解することが重要です。ここでは、平方根、解の公式、因数分解の3つの基本的な解法を詳しく解説し、それぞれの方法を使った演習問題を紹介します。

1-1.二次方程式とは

二次方程式は、数学において非常に重要な方程式の一つです。

その一般的な形はax²+bx+c=0で表されます。

ここでは、aは0ではない実数、b、cは任意の実数、そしてxは未知数（変数）です。

問題としては以下のような形で出題されます。

例）下記の式のxの値を求めよ

2x²-7x+3=0

このように二次方程式は、xが二乗の項を含み、三乗以上の項を含まない方程式のことです。

二次方程式は、多くの実世界の問題を数学的に表現するのに適しています。 たとえば物体の運動、面積や体積の計算、経済モデルなど、さまざまな分野で活用されています。

1-2.二次方程式の解法3パターン

二次方程式を解くためには、主に3つの方法があります。それぞれの方法には適用するべき状況や利点がありますので、ここではその3つのパターンを詳しく見ていきましょう。

1-2-1.平方根

平方根を用いる方法は、最もシンプルな形の二次方程式を解く際に使用します。

具体的には、x²=k（kは定数）の形の方程式に適用されます。 この方法では、両辺の平方根をとること（何の2乗になるか）で解を求めます。

たとえば、x²=16という方程式を考えてみましょう。 両辺の平方根をとると、x=±4となります。 つまり、x=4またはx=-4が解となります。

この方法の利点は、計算が非常に簡単であることです。 しかし、適用できる方程式の形が限られているという制限があります。

1-2-2.解の公式

解の公式は、あらゆる二次方程式を解くことができる強力な公式です。

一般形ax²+bx+c=0の二次方程式の解は、x=[-b±√(b²-4ac)]/(2a)という公式で求められます。 この公式は、どのような二次方程式にも適用できるため、非常に便利です。

解の公式を使う際は、まず方程式の係数a、b、cを特定します。 そして、これらの値を公式に代入して計算を行います。 ±の記号があるため、通常は2つの解が得られます。

たとえば、2x²-7x+3=0という方程式を解いてみましょう。 ここでは、a=2,b=-7,c=3です。 これらの値を公式に代入すると、x=[7±√(49-24)]/4となります。

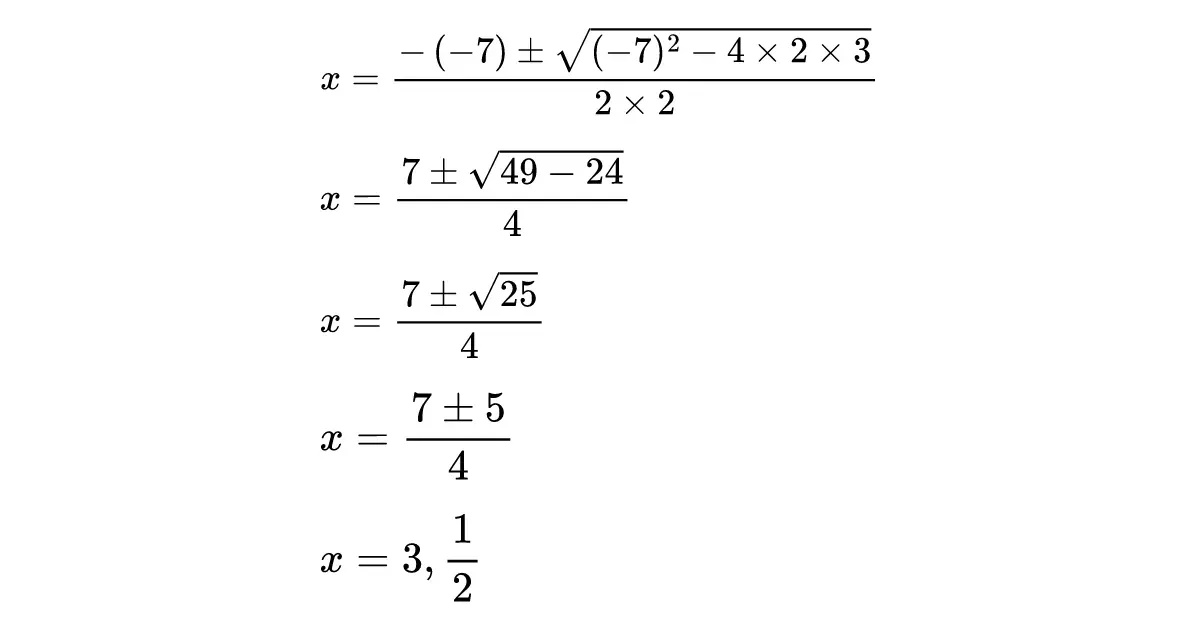
計算を進めると、x=3またはx=1/2という解が得られます。

1-2-3.因数分解

因数分解は、2次式を1次式同士の掛け算に分解することです。 因数分解ができれば、解の公式と比べて計算が簡単になる、という利点があります。

因数分解の基本的な考え方は、ax²+bx+c=0を(x+p)(x+q)=0の形に変形させることです。

たとえば、x²+6x+8=0という方程式を解いてみましょう。 足して6・掛けて8の数字は2と4なので、この方程式は(x+2)(x+4)=0と因数分解できます。

因数分解ができたら、x+2=0またはx+4=0を解くことで、x=-2またはx=-4という解が得られます。

ただし、すべての二次方程式が簡単に因数分解できるわけではありません。 特に、係数が整数でない場合は因数分解が難しくなることがあります。 そのような場合は、解の公式を使用します。

1-3.二次方程式の解き方の流れ

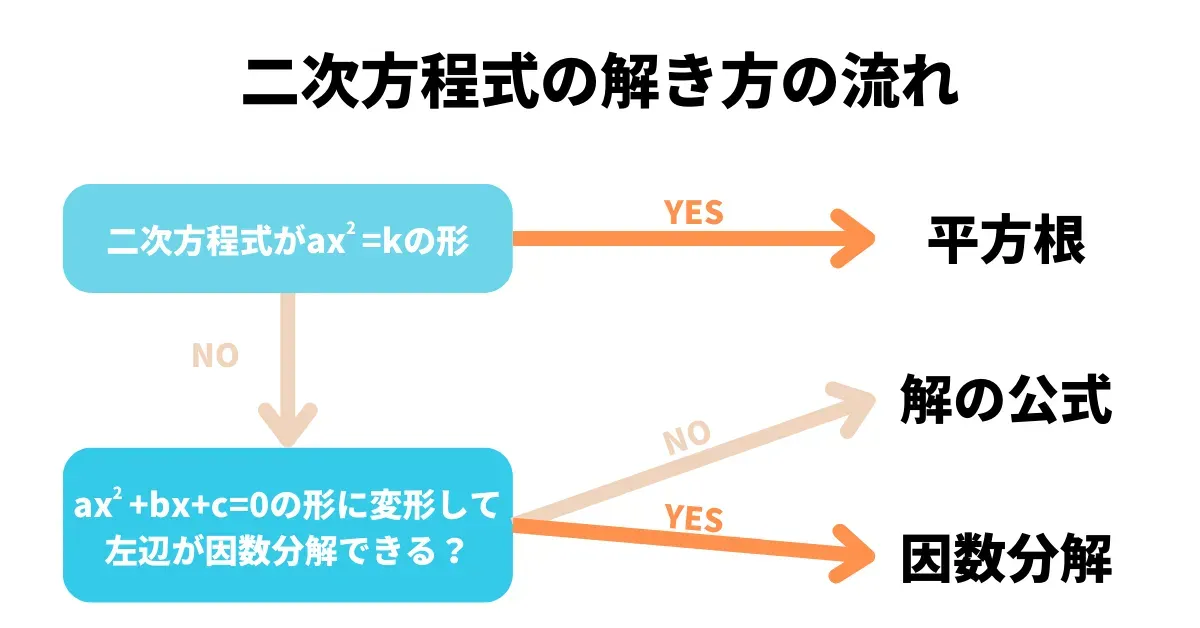
二次方程式を素早く正確に解くためには、適切な解法を選択することが重要です。 ここでは、効率的に二次方程式を解くための理想的な流れを紹介します。

1. まず、与えられた方程式がx²=kの形であるかを確認します。 この形であれば、平方根を使う方法が最も簡単です。 そうでない場合は、次のステップに進みます。
2. 方程式の右辺を0に整理し、ax²+bx+c=0の形にします。
3. 因数分解が可能かどうかを試します。 因数分解ができれば、それを用いて解を求めます。 因数分解は、計算が比較的簡単で、正確に素早く計算できるという利点があります。
4. 因数分解が難しい場合や、すぐに因数分解の形が思いつかない場合は、解の公式を使用します。 解の公式は、どのような二次方程式でも解くことができる万能な方法です。 a,b,cの値を特定し、x=[-b±√(b²-4ac)]/(2a)の公式に代入して解きます。

ポイントは、安易に解の公式に頼るのをやめることです。 解の公式は、すべての二次方程式を解ける一方で、計算が複雑でミスをしやすいです。 そのため平方根の形にならず、因数分解もできない場合にのみ活用するようにしましょう。

この流れに従うことで、各方程式に対して最も適した解法を選択し、効率的に問題を解くことができます。

2.二次方程式の練習問題

2-1.平方根で解く二次方程式の演習問題

平方根を用いて解く二次方程式をしっかり解けるようにしていきましょう。 演習問題を通じて、平方根を使った解法を練習してみましょう。

解答

1. x=±5
2. x=±4
3. x=±5

2-2.解の公式で解く二次方程式の演習問題

解の公式は、どんな二次方程式にも適用できる強力なツールです。 実際の問題を解くことで、公式の使い方をマスターしましょう。

解答

1. x=(-3±√17)/4
2. x=(3±√5)/2
3. x=(5±√37)/6

2-3.因数分解で解く二次方程式の演習問題

因数分解を用いた解法は、二次方程式を素早く正確に解くための方法です。 演習問題で、因数分解を練習して素早く解を見つける方法を習得しましょう。

解答

1. x=-2またはx=-3
2. x=5またはx=-2
3. x=-4またはx=2

2-4.二次方程式の練習問題5選

これまでに学んだ解法を総合的に活用する練習問題を5問用意しました。 さまざまな形式の問題に挑戦することで、解法の理解を深め、実践力を養いましょう。

解答

1. x=-5またはx=3（因数分解を利用）
2. x=±2√2（平方根を利用）
3. x=-6またはx=2（因数分解を利用）
4. x=2または1/3（解の公式を利用）
5. x=-7またはx=2（因数分解を利用）

3.複雑な二次方程式の解法

二次方程式の基本的な解法をマスターした後は、応用パターンに挑戦してみましょう。 ここで紹介するパターンは、より複雑な式からなる二次方程式です。 実際の問題を通じて理解を深めていきましょう。

3-1.二乗の項に係数が含まれているパターン

二次方程式の中にはx²の係数（文字に掛けられている数）が1でないものもあります。 たとえば、3x²や5x²となっている場合です。 そうした二乗の項に係数が含まれている二次方程式の解き方を解説します。

まず、すべての項が共通の因数で割れるかどうかを確認します。 もし割れない場合は、解の公式を使用して解を求めましょう。

1.すべての項が共通の因数で割れる場合

たとえば、2x²-4x+2=0という方程式を考えてみます。 この方程式のすべての項は2で割ることができます。

2x²-4x+2=0 両辺を2で割ると、x²-2x+1=0になる。

このようにしてx²の係数を1にすると、因数分解が可能になる場合があります。 この例では、(x-1)(x-1)=0と因数分解でき、解はx=1となります。

2.共通の因数で割れない場合：

たとえば、3x²-5x-1=0のような方程式では、共通の因数で割ることができません。 このような場合は、解の公式を使って解きましょう。

x=[-b±√(b²-4ac)]/(2a)の解の公式に代入して解きます。 この例では、a=3,b=-5,c=-2となり、解はx=(5±√37)/6になります。

3-2.置き換えを使って解くパターン

置き換えを使うことで問題を簡単にできる二次方程式もあります。 たとえば、(2x-1)²=9のような方程式です。

置き換えの基本的な考え方は、複雑な部分を新しい変数で表現し、方程式を単純な形に変形することです。 上記の例では、y=2x-1と置き換えることで、y²=9という簡単な方程式に変換できます。

この方法の利点は、複雑な方程式を扱いやすい形に変換できることです。 ただし、最後に元の変数xに戻すことを忘れないよう注意が必要です。

3-3.複雑な二次方程式の練習問題

複雑な二次方程式の練習ができる問題を4つご用意しました。 問題に挑戦して、複雑な二次方程式も解けるようにしていきましょう。

解答

1. x=2（両辺を2で割る）
2. x=2,1/3（解の公式を利用）
3. x=2,-2/3（置き換えを利用）
4. x=0,2（置き換えを利用）

中学数学の効率のよい勉強方法

中学数学を効率よく学ぶためには、基本的な概念の理解から応用問題の解決まで、バランスよく取り組むことが重要です。 ここでは、数学の基礎をしっかり固める方法から、応用力を養うための具体的な勉強方法までを紹介します。

単語や文法、長文、リスニングなど多岐にわたる分野の力が求められる英語と違い、数学は問題集をしっかり練習することで学力を高めていける教科です。

これらの方法を実践することで、数学の学力を着実に向上させることができます。 二次方程式はもちろん、ほかの単元も確実に勉強していきたいところです。 数学全般の勉強法について詳しく解説します。

基礎固めの重要性

数学では基本概念を理解することが極めて重要です。

複雑な問題を解くための土台を築き、応用力を養うためには基本概念を理解することが重要だからです。

たとえば方程式を学ぶ際、単に解き方を暗記するのではなく、「等式の性質」を理解することが大切です。「両辺に同じ数を足しても引いても等式は成り立つ」という性質を理解すれば、方程式の解き方もしっかり理解できるようになります。

教科書の説明を丁寧に読み、わからない部分は積極的に質問しましょう。

計算練習を徹底する

テストで安定して点数を取るためには計算ミスを減らすことが大切です。

計算ミスが多くなると、理解できていたはずの問題も失点につながってしまうからです。

計算ミスを減らすためには、日々の計算練習が欠かせません。

計算力が身についていれば、問題を解くスピードも向上し、テストでの時間配分にも余裕が生まれます。

問題集を繰り返し解く

数学の理解を深めるためには、問題集を繰り返し解くことが重要です。

同じ問題を何度も解くことで、公式や解法のパターンを自然に覚えることができるからです。

特に間違えた問題は重点的に復習し、同じミスを繰り返さないようにしましょう。

何度も繰り返し問題を解くことで、テストで｢同じ問題だ！｣と感じて答えられるようになります。

理解を優先する

数学では理解を優先することが大切です。 公式や定理をただなんとなく暗記するのはNGな勉強法です。

公式や定理の背景にある理論を理解することで、定着につなげられたり、もし忘れてしまったときも自分で導出できたりするからです。

たとえば、円の面積公式である「πr²」も単に暗記するのではなく、その導出過程を理解するようにしましょう。

学校や塾の授業などの解説をしっかり理解することから、学習をスタートしましょう。

必要な部分は暗記する

数学では理解を重視しつつも、必要な部分はしっかりと暗記することも重要です。

公式や重要なポイントを覚えることで、試験の際にスムーズに解答できるからです。

今回の記事で解説した、二次方程式の解の公式「x=(-b±√(b²-4ac))/2a」は、その導出過程を理解したうえで、しっかり暗記しておくとよいでしょう。

試験の際にスムーズに解答できるようになり、時間の節約にもつながります。

過去問を活用する

過去問を活用することは、定期テスト対策において非常に効果的です。

過去のテスト問題を解くことで、出題傾向を把握しやすくなり、自分の弱点を発見できます。

たとえば図形の問題が多く出題されていることに気づいたら、その分野を重点的に復習することができます。

また過去問を時間を計って解くことで、本番の試験でのペース配分の練習にもなります。

1日の終わりに復習する

1日の終わりに復習することは、学んだ内容を記憶に定着させるために効果的です。

その日に学んだ内容を寝る前にもう一度確認することで、短期記憶から長期記憶に移行しやすくなるからです。

毎日の復習を習慣化することで、学習内容がしっかりと身につきます。

定期的な総復習

定期的な総復習を行うことで、学習内容の定着度を高めることができます。

過去に学んだ内容を振り返ることで、忘れていた知識を再確認できるからです。

具体的には、週末に1週間分の内容を復習するのがおすすめ。 ノートを見直したり、間違えた問題を解き直したりすることで、長期的な記憶につなげられます。

復習を習慣化することで、着実に学力を向上していきましょう。

まとめ

二次方程式は中学数学における重要なテーマであり、その解き方をマスターすることはほかの数学分野にも大きく影響します。

本記事では、二次方程式の解き方を3つの基本的な方法（平方根、解の公式、因数分解）に分けて解説しました。また、それぞれの方法を使った練習問題もご紹介しました。

二次方程式の解き方を習得するためには、基本的な解法を理解し、適切な方法を選んで練習を繰り返すことが重要です。

そして、数学全般の効率的な勉強法も紹介しました。 基礎固め、計算練習、問題集の繰り返し、理解を優先する学習、必要な部分の暗記、過去問の活用、毎日の復習、定期的な総復習などのやり方を解説しました。

これらの方法を実践することで、二次方程式のみならず、中学数学全般の成績を向上させることができます。

この記事を参考にして、日々の学習を効率的に進めてください。皆さんの数学の学習がより楽しく、成果のあるものになることを願っています。