三平方の定理（ピタゴラスの定理）とは？一瞬で解ける裏ワザも紹介

中学3年生の秋ごろに習う三平方の定理。中学数学の集大成として習う単元であり、ここでつまずいてしまう中学生もいるのではないでしょうか？

三平方の定理は「直角三角形の辺の長さ」がわかる数学のきまりです。

この記事では、この三平方の定理の使い方や、計算方法、そしてこの定理を使った応用問題の解き方などを解説します。ぜひ数学の勉強にお役立てください。

三平方の定理とは？

三平方の定理の基本概念

三平方の定理とは、直角三角形の3辺の長さの間に成り立つ関係について述べた定理です。定理を発見した古代ギリシャの数学者ピタゴラスの名前を用いて、「ピタゴラスの定理」と呼ばれることもあります。

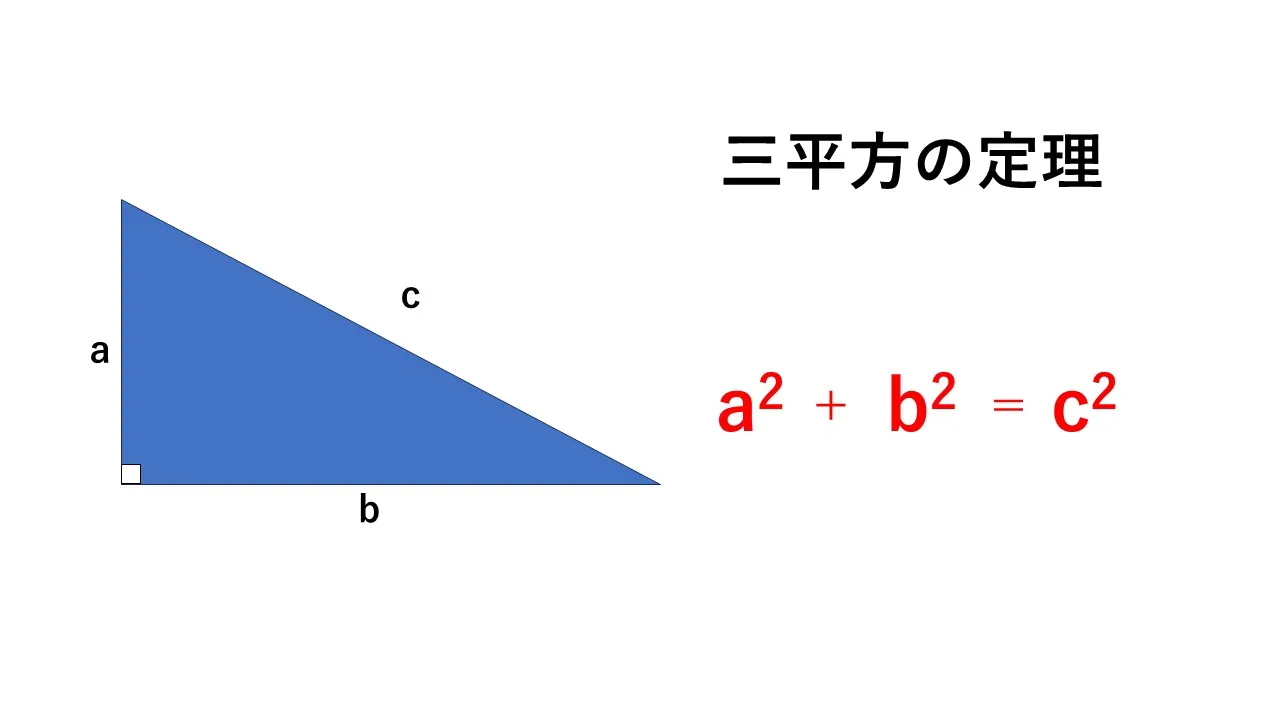
この定理は、直角三角形で直角を挟む2辺の長さをそれぞれ a、b、そして斜辺（直角の向かい側の一番長い辺）の長さを c とすると、次のような関係が成り立ちます。

「a² + b² = c²」

三平方の定理を使えば、直角三角形で2つの辺の長さが分かっている場合に残り1つの辺の長さを計算で求めることができます。逆に、3辺の長さが与えられた三角形について、その長さがこの関係を満たしていれば（つまり、a² + b² = c² が成り立てば）、その三角形は直角三角形であるといえます。

例えば、辺の長さが 3、4、5 の三角形では

3² + 4² = 5²（9 + 16 = 25）

が成り立つため、直角三角形であることがわかります。

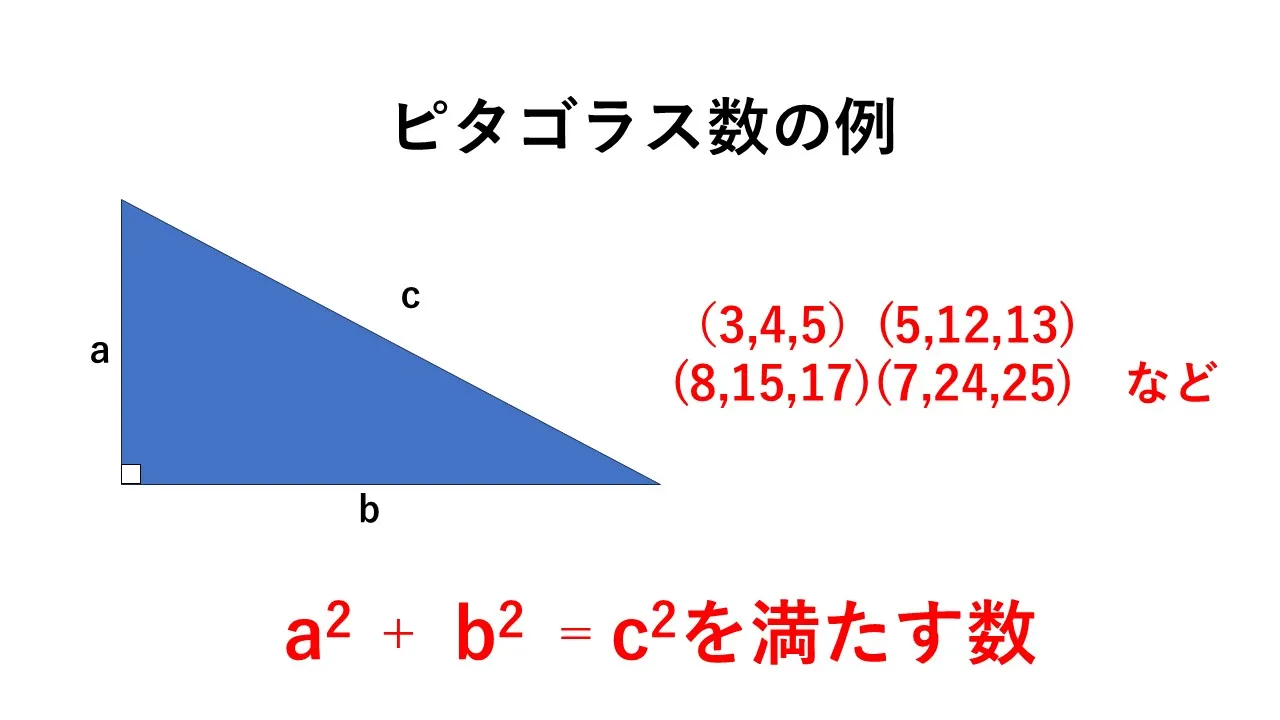
このように整数のみで三平方の定理が成立する3つの数の組み合わせをピタゴラス数（ピタゴラスの三つ組）と呼びます。この「ピタゴラス数」は、「3、4、5」のほかにも「5、12、13」「7、24、25」などが挙げられ、高校受験をする受験生の中にはこのピタゴラス数の組み合わせを覚えている人も少なくありません。

この「三平方の定理」は中学数学の集大成ともいえる重要な定理で、シンプルな計算問題だけでなく、平面図形から空間図形にまで幅広く登場します。
次に紹介する証明方法を見ながら、この定理が本当に成り立つ理由を確認してみましょう。

三平方の定理の証明方法

三平方の定理には非常に多くの証明方法が知られています。ここでは代表的な2つの証明を紹介します。

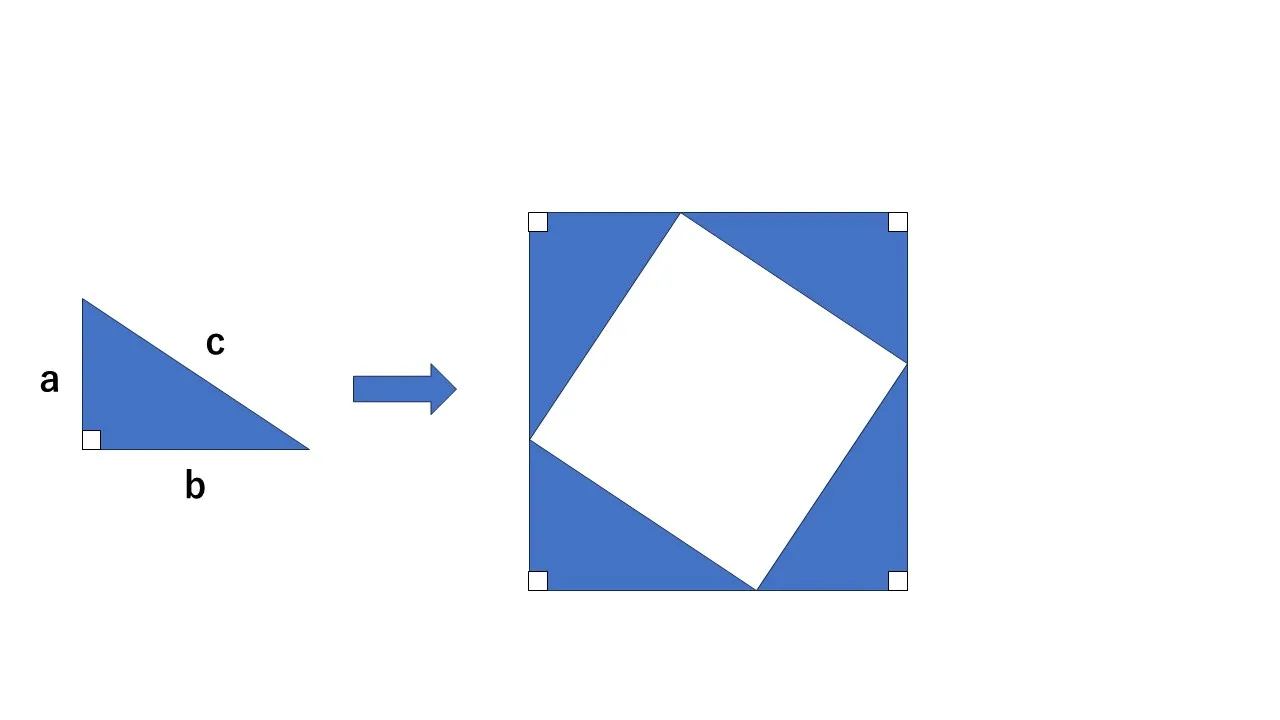
①図形の面積を利用した証明

上の図のように、辺の長さが a、b、の直角三角形を4つ用意し、大きな正方形の中に隙間なく並べてみます。大きな正方形の一辺の長さは「a+b」となり、中央の空いた部分が一辺「c」の正方形になります。このとき、次のような面積の関係が成立するのです。
「大きな正方形の面積 = 小さな正方形の面積 + 4つの直角三角形の面積」

これを式で表すと次のようになります。
(a+b)² =  c² + 4 × 1/2 ab
左辺は大きな正方形の面積です。一辺の長さがa+bであるため、面積は(a + b)²となります。
右辺は、中央の小さな正方形の面積（c²）と、その周りにある4つの直角三角形の合計です。

1つの直角三角形の面積は1/2×a×bで、4つあるため4×1/2×abとなります。
この式を展開して整理をすると次のようになります。

左辺の展開　(a+b)²＝a² +2ab+b²
右辺の展開　c²＋4×1/2ab=c²+2ab

したがって　a² +2ab+b²＝c²+2ab
両辺から2abを引くとa² + b² = c²

となるため、三平方の定理が成立することが示されました。
この証明方法は、図形を使って面積の関係式をつくり、直感的にもわかりやすいため「ピタゴラスの定理の証明」の中で広く知られているものの1つです。

②三角形の相似を利用した証明

もう一つは、直角三角形内に線を引いてできる、相似の関係にある図形を使う方法です。

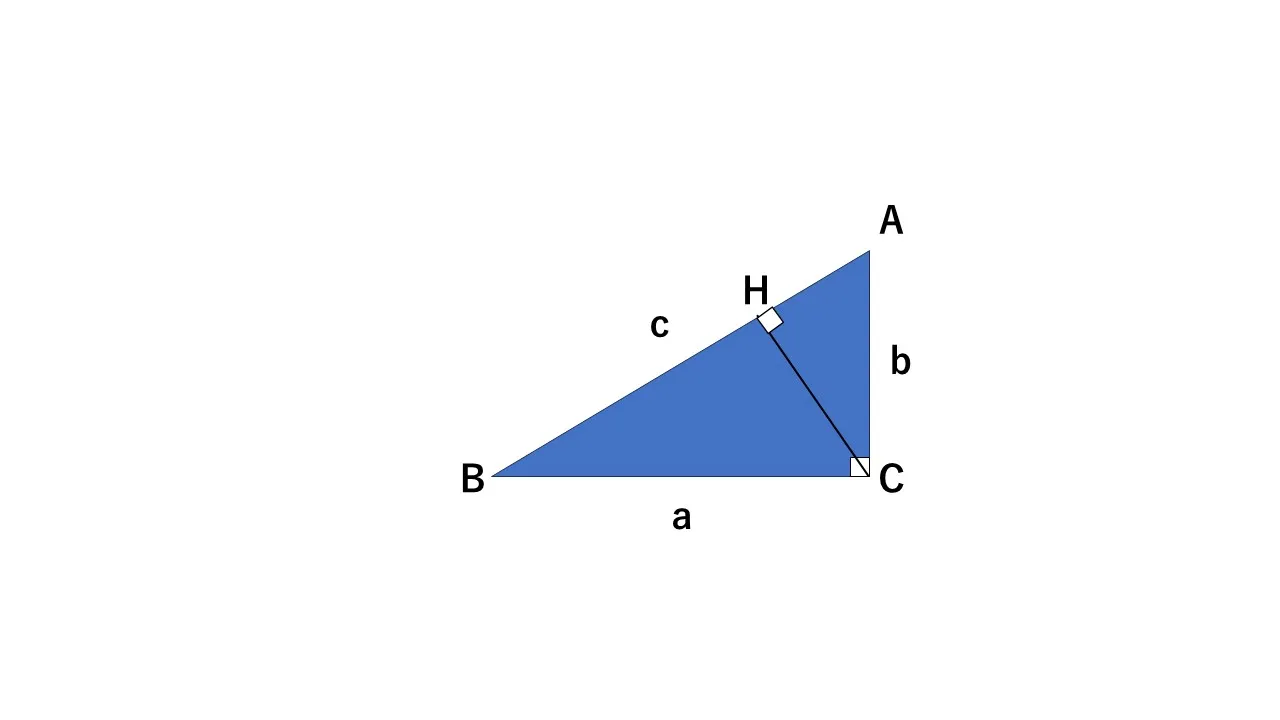
こちらの図を見てみましょう。

直角三角形の直角（角C）から斜辺に垂線を下ろし、斜辺ABをAH、BHという2つの線分に分けます。すると、できる小さな2つの直角三角形（△ACH、△CBH）は、元の大きな直角三角形△ABCと3つの角度が全て等しいため相似になります。

相似な図形の各辺の長さの比は等しくなるため、その性質を利用すれば「辺AH」「辺BH」の長さを「a,b,c」を用いて表すことができます。

例えば小さい三角形の一つについて辺の比から
AH = b × b/c
もう一方は
BH = a × a/c

となります。斜辺全体の長さである「c」の値は「AH + BH」と等しくなるため、
c =  b × b/c + a × a/c

となり、両辺に「c」をかけて左辺、右辺を入れ替えると
a² + b² = c²
が得られます。このように、相似な図形の辺の長さの比を考えることで、代数的に三平方の定理を証明することができるのです。

こちらの方法は計算を要しますが、図形の性質（相似）を利用した美しい証明といえるでしょう。今回は斜辺ABの長さに着目しましたが、他の辺を用いて立式しても同様に証明することができるため、ぜひやってみてください。

「三平方の定理」は多くの数学者がその証明に熱狂しているテーマであり、今回紹介した2つの証明方法のほかにも、円を用いた証明や動的な図形の分割を使った証明など、世界中で100種類以上の証明が考案されています。興味がある人はぜひ調べてみてください！

三平方の定理の応用

三平方の定理は、平面上の図形だけでなく空間図形の問題にも応用できます 。ここでは典型的な応用例として、円の弦（弧を結ぶ線分）の長さを求める問題と、立体（直方体や立方体）の対角線の長さを求める問題を見てみましょう。

三平方の定理で弦の長さを求める

円の弦の長さとは、円周上の2点を結ぶ線分の長さです。円の中心から離れた位置にある弦の長さは、三平方の定理を使うことで求めることができます。

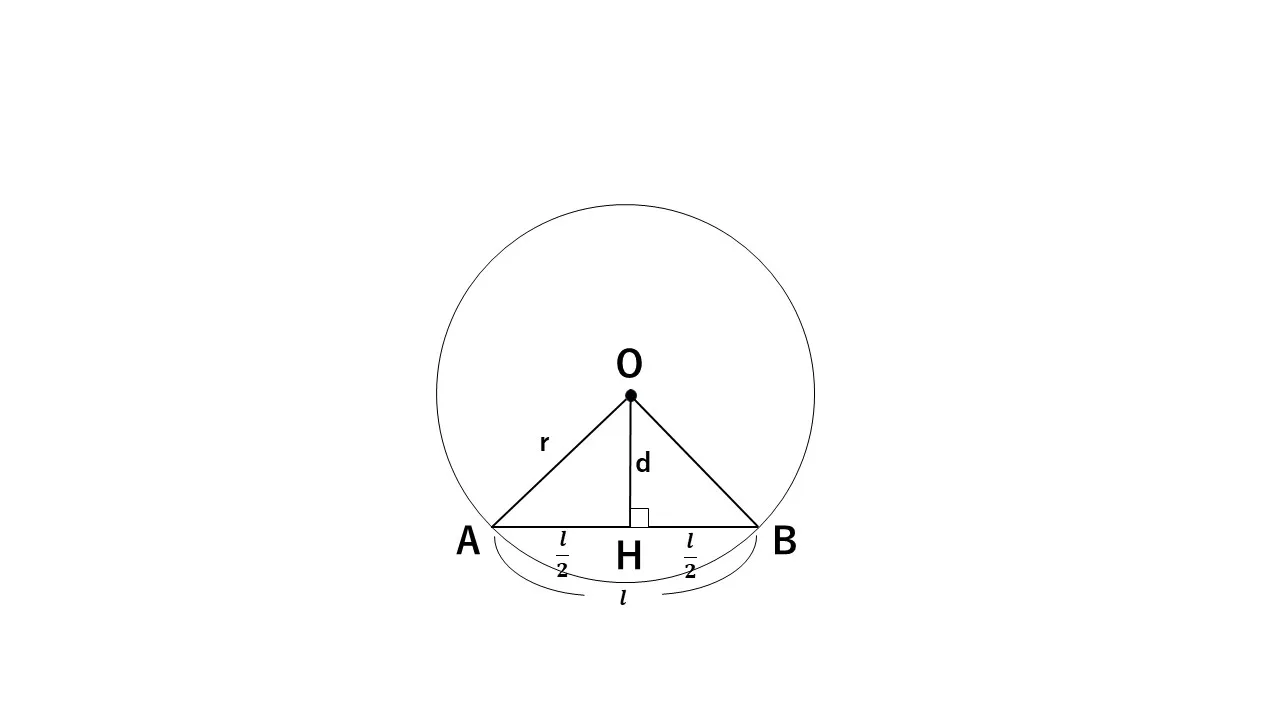
ポイントは、円の中心Oから弦ABに垂線（垂直な線）を下ろすことです。

上の図をご覧ください。垂線と弦の交点をHとすると、OHは弦ABをちょうど二等分します。よって、AH = HBとなり、「AH」「HB」の長さはともに弦ABの半分となります 。

このとき三角形 OAH に注目すると、∠OHAが90°の直角三角形になっています。円の半径を「r」、中心から弦までの距離（OHの長さ）を 「d」、求める弦の長さを「l」としましょう。

ここで、AH は弦の半分であるため、長さは「l/2」 となります。同じく OA は半径なので長さは「r」、OH は「d」です。ここで、直角三角形 OAH に三平方の定理を適用すると、次の式が成り立ちます。

(l/2)² + d² = r²

これを解くと、

(l/2)² = r² - d²

となり、弦の長さを求められます。

例えば半径5cmの円で、円の中心からある弦までの距離（垂線の長さ）を3cmとしましょう。このとき弦の長さ「l」は、上の式から次のように表すことができます。

l =√( 5² - 3²) ×2 = 8（cm）

このように三平方の定理を使えば、円に内接する三角形の問題で弦の長さや弦までの距離を計算で求めることが可能です。

三平方の定理で立体の対角線を求める

三平方の定理は立体図形にも応用できます。直方体や立方体の対角線の長さを求めるのにも利用されています。

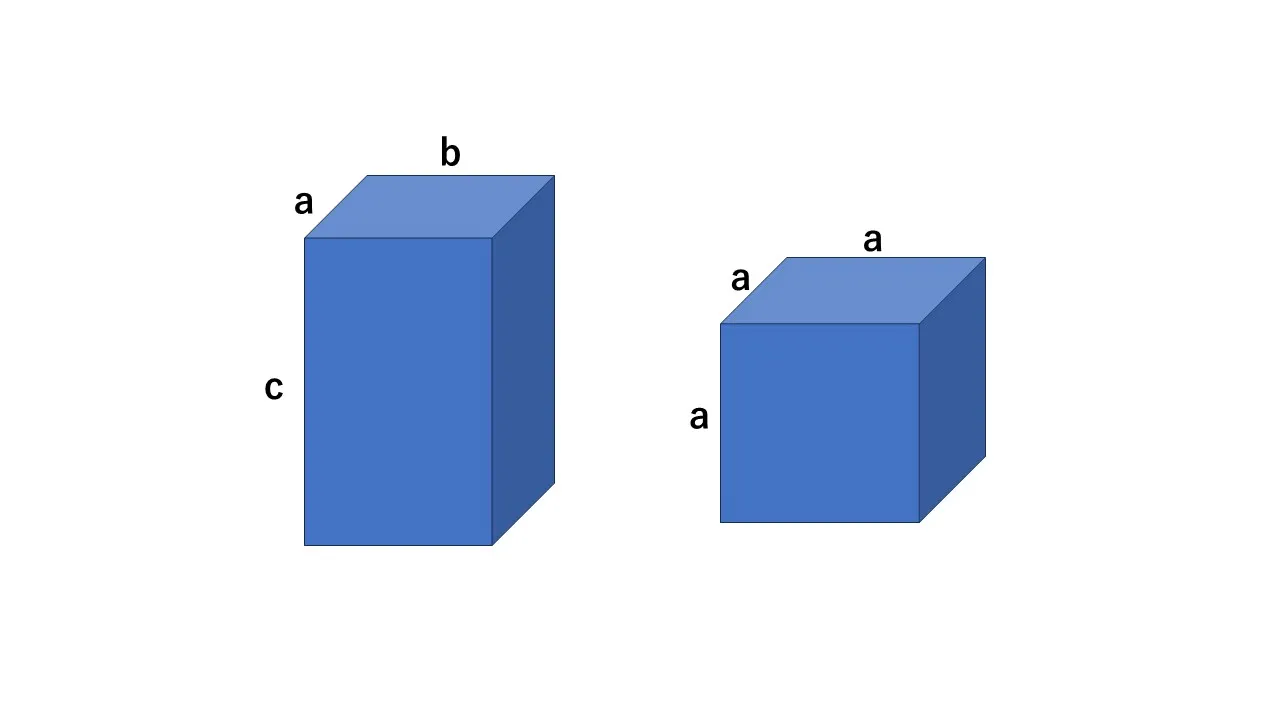
まず直方体の場合を考えてみましょう。縦が a、横が b、高さが c の直方体をイメージしてください。この直方体の対角線とは、立体の中を対角に貫く線分、つまり片方の底面の隅から、反対側の上面の隅へ伸びる線分のことです 。この対角線の長さを求めるには、一度平面の対角線を求め、それを斜め上方向にもう一度対角線として考えるとよいでしょう。

そのために、まず底面の長方形で対角線の長さを出します。底面の対角線の長さは三平方の定理で √（a²+b²） となります。次に、その対角線を一辺、そして高さ c をもう一辺とする直角三角形を考えると、立体の対角線は次のように式で表すことができます。

d² = (√（a²+b²）) ² + c² = a² + b² + c²

直方体の対角線の長さは「d」とおくと

d = √(a² + b² + c²)

と求めることができるのです。

具体的な数字で考えてみましょう。

例えば、縦3cm・横4cm・高さ12cmの直方体であれば、その対角線の長さdは次のように求めることができます。

 d = √(3² + 4² + 12²) = √(9+16+144) = √169 = 13(cm)

このように、三平方の定理を応用することで、立体の対角線も簡単に求めることが可能です。

次に立方体の場合を考えてみましょう。実は、立方体は直方体よりも簡単に対角線の長さを求めることができます。

立方体は縦横高さすべて同じ長さであるため、その長さを「a」とおくと、対角線の長さd は次のような式で表すことができます。

d = √(a² + a² + a²) = √(3a²) = √3 a

例えば一辺が10cmの立方体であれば、対角線は10√3 cm（約17.3cm）となります。このように三平方の定理を二次元→三次元へと拡張して使うと、立体の長さも公式的に計算で求めることが可能です。

三平方の定理の裏ワザ

三平方の定理は便利な公式ですが、「二乗して和を取って平方根を取る」という計算は少し手間がかかります。

ここからは、計算を簡単にしたり、素早く解いたりするための裏ワザを紹介します。数学が苦手な人でも使えるテクニックであるため、ぜひ覚えてみましょう。

①2つの三角定規の性質

この記事を読んでいる方の多くは、かつて学校で「三角定規」というものを使ったことがあるでしょう。日本の学校で使われているプラスチック製の三角定規は、どちらも代表的な直角三角形となっています。三角定規は直角三角形の辺の長さが決まっているため、三平方の定理を実際に目で見て確認する道具として便利です。

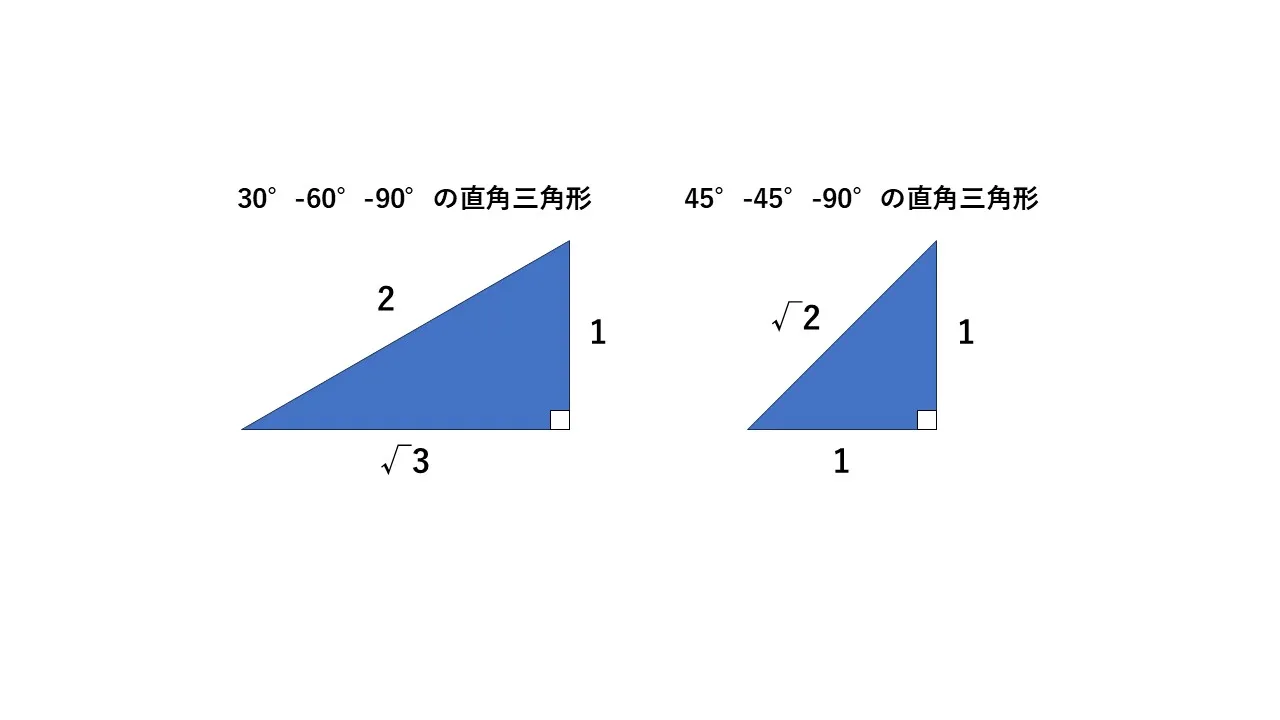
1つは角度が45°-45°-90°の直角二等辺三角形、もう1つは30°-60°-90°の直角三角形です。

直角三角形では辺の長さの比が決まっており、45°-45°-90°の三角形は辺の比が「1：1：√2」（斜辺が他の辺の√2倍） 、30°-60°-90°の三角形は辺の比が「1：√3：2」（30°に対する辺：60°に対する辺：斜辺 = 1：√3：2） となっています。

つまり、これら特別な角度を持つ直角三角形では、一辺の長さが分かれば他の辺の長さも比から簡単に求められるのです。

例えば、45°-45°-90°の直角二等辺三角形で一辺の長さが5 cmとわかれば、もう1辺も同じ5 cm、斜辺は 5 √2cm(約7.07 cm) と求められます。

もう一つの30°-60°-90°の直角三角形であれば、例えば斜辺が10 cmとわかれば、短い直角側（30°に隣接する辺）はその半分の5 cm、長い直角側（60°に隣接する辺）は 5√3cm(約8.66 cm )と求められます。

このように、三角定規と同じ形の直角三角形では辺の長さを比を用いて計算できるため、三平方の定理を使わなくても辺の長さを素早く求めることができるのです。

②1辺しかわからないときは角度に注目

直角三角形の問題で一辺の長さしか与えられていない場合、必ずどこかに角度に関する情報があるはずです。

特に「30°」「45°」「60°」といったおなじみの角度が出てきたら要注目です。先ほど述べたように、それらの角度を持つ直角三角形では辺の比があらかじめ分かっているので、角度から三角形の形を特定し、辺の比で計算すると簡単に問題を解くことができます。

例えば、「直角三角形で1辺の長さしか分からないけれど30°の角がある」という問題なら、その直角三角形は30°-60°-90°型です。三角形の3つの内角の和は180°であることが分かっているため、残りの1つの角度を次の式で求めることができます。

180°-(90°+30°) = 60°

30°-60°-90°型とわかれば辺の比は 1：√3：2 であるため、与えられた1辺をこの比に当てはめて他の辺を求めることができます。ある直角三角形の斜辺が10√3 cmで角度が30°を含むなら、斜辺に対応する比が2に当たるので他の辺はそれぞれ下記のように求めることが可能です。

10√3 ÷ 2 = 5√3 (cm)

5√3 ×√3 = 15(cm)

角度の情報を見逃さず、「三角定規の形かも？」と考える習慣をつけておくと、与えられた一辺だけで直角三角形の残りの辺を導き出すことが可能です。

※補足：もし特殊な角度でない場合（例えば問題文に角度が明記されていない場合）は、三平方の定理だけでは1辺から他の辺を求めることはできません。その場合は別途角度を求める工夫や三角比（サイン・コサイン）の知識が必要になりますが、中学範囲では上記のような特別な直角三角形のパターンを押さえておけば十分対応できます。

③ピタゴラス数を覚えておく

ピタゴラス数とは、三平方の定理を満たす三つの整数の組合せのことです。最も有名なものは 「3、4、5」 で、この他にも 「5、12、13」, 「8、15、17」, 「7、24、25」など重要な組合せがいくつかあります。

テストや問題集では、こうした覚えやすい整数の組が直角三角形の辺の長さとして登場することが多いです。なぜなら、計算結果が整数になるため解答がきれいにまとまりやすいからです。

例えば、問題で

「ある三角形の辺の長さが7、24、25である。この三角形は直角三角形か？」

と聞かれたとします。このとき

7² + 24² = 49 + 576 = 625

25² = 625

であるため三平方の定理が成り立ち、直角三角形であるとすぐ判断できます。

もしピタゴラス数を知らなければ二乗の計算から始めなければなりませんが、覚えていれば暗算レベルで直角かどうかの判定ができるわけです。頻出の「3、4、5」はもちろん、上記のような組合せはテスト前に暗記しておくことをおすすめします 。

④斜辺ともう1辺の長さがわかっているときは計算が楽になる

直角三角形の斜辺と他の1辺の長さが与えられた場合、普通の解き方であれば、「2つの辺の長さを2乗してからその差を取り、最後に平方根を取る」という計算になります。もちろんこの方法で残りの辺の長さを求めることはできますが、数字も大きいため計算が複雑になり、計算ミスをすることもあるでしょう。

このようなときは、「因数分解」を活用しましょう。具体的には、三平方の定理の式を変形した b² = c² - a² = (c+a)(c-a)を用います。

例えば斜辺の長さが37、他の一辺が35の場合、通常は「37² - 35²」を計算して平方根を取ります。「37」の2乗、「35」の2乗はそれぞれ4けたの数になり、かなり計算に時間がかかってしまうでしょう。ここで因数分解を使うと、次のような式になります。

37² - 35² = (37+35)(37-35) = 72×2 = 144

この式から平方根を取れば答えは12と導くことができます。2乗を2回計算するよりは確実に早く計算できそうですよね？

この因数分解のテクニックを活用すると、2乗の計算を「和」と「差」の積に直せるため計算が楽になります 。計算ミスも減らすことができるため、斜辺と他の一辺が与えられたら「和×差」を考えてみましょう。

もちろん、すべての問題で使用する必要はありませんが、この裏ワザを知っておくだけでも、斜辺が絡む計算をスムーズに処理することができます。ぜひ活用してください！

三平方の定理を使ってみよう

それでは実際に、三平方の定理を使う練習問題を解いてみましょう。初歩的な問題から少し応用的な問題まで、丁寧に解説しながら確認します。三平方の定理をきちんと理解するためにも、一度自分で考えてから解説を読んでみてください。

問題1: 直角三角形の斜辺以外の2辺の長さが 6cm と 8cm です。斜辺の長さを求めなさい。

解説: 直角を挟む2辺の長さが「6cm」と「8cm」であるため、三平方の定理から斜辺の長さ「c」は次のような式になります。

c =√(6² + 8²) = √(36+64) = √100 = 10(cm)

計算過程で 「6² + 8² = 10²」という関係が出てきましたが、これは「3,、4、5」のピタゴラス数を2倍した組合せとなっています。裏技を覚えていた人は計算を待たずとも答えを出すことができたかもしれませんね。

問題2: 3つの内角の大きさがそれぞれ「30°-60°-90°」の直角三角形があります。一番短い辺の長さが3cmのとき、残りの2つの辺の長さを求めなさい。

解説:「30°-60°-90°」の直角三角形の辺の長さの比は、「1：√3：2」と分かっています。これを用いると、一番短い辺の長さがわかっているため、斜辺の長さは次の式で表すことができます。

3×2 = 6(cm)

もう一つの辺の長さは次のような式になります。

3×√3 = 3√3(cm)

三角定規と同じ形の直角三角形の性質を覚えておくことで、三平方の定理を使わなくても1つの辺の長さから他の辺の長さを求めることができます。

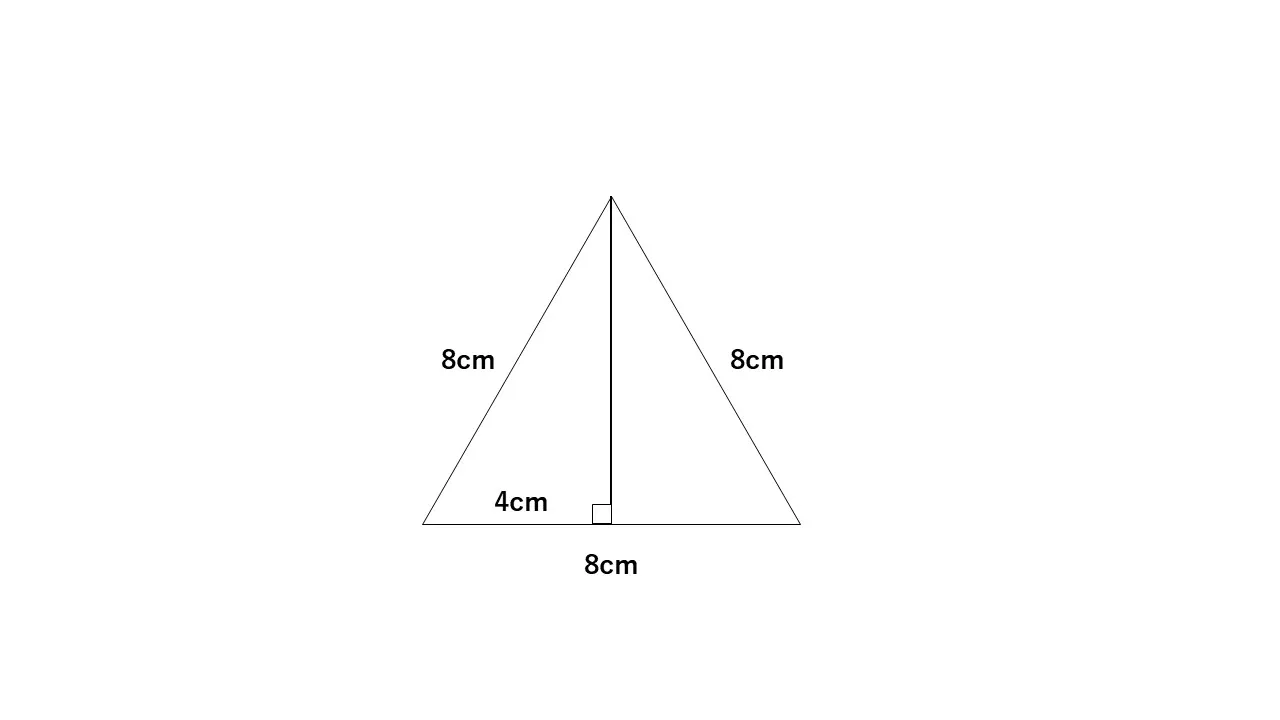
問題3: 1辺の長さが8cmの正三角形があります。その面積を求めましょう。

解説: もしかしたらこの問題を見て、「え、これも三平方の定理なの？」と思ったかもしれません。そのような人は、図形に補助線を引いて考えてみましょう。

正三角形の一つの頂点からその対辺に垂線を引くと、正三角形を2つの直角三角形に分けることができます。この三角形は「30°-60°-90°」の特殊な直角三角形であるため、「1,√3,２」の辺の長さの比を用いて、正三角形の高さを次の式で求めることができます。

4×√3 = 4√3(cm)

あとは三角形の面積の求め方である「底辺×高さ÷2」に当てはめて式をつくりましょう。

8×４√3÷2 = 16√3(cm²)

三平方の定理を応用して、1辺の長さがわかっている正三角形の面積を求めることができます。

 「直角三角形かな？」と気づくこと、そして公式を正しく当てはめることがポイントです。

計算ミスを防ぐため、2乗や平方根の計算にはくれぐれも注意しましょう！

三平方の定理の重要ポイントをおさらい

ここまで、三平方の定理の成り立ちからその使い方、実際の問題について順番に解説していきました。最後に、三平方の定理の重要ポイントをおさらいしましょう。

①基本公式

直角三角形において「斜辺の長さの二乗 = 他の2辺の長さの二乗の和」、つまり3つの辺の長さを「a,b,c」としたとき、「a² + b² = c²」となる。この関係をしっかり覚えましょう。

公式を丸暗記するのではなく、正方形の面積など、図を使った三平方の定理の導出の仕方も覚えておくと理解しやすいです。

②裏ワザ活用

「30°-60°-90°」や「45°-45°-90°」などの特殊な角度の直角三角形では、辺の比を利用して計算を簡略化することができます。

また、「3,4,5」「5,12,13」などの組み合わせはピタゴラス数と呼ばれる直角三角形となる数の組み合わせとなります。問題の状況に応じて計算の工夫をすると解答スピードが上がり、計算ミスも減らすことができます。

③応用力

三平方の定理は円や立体にも応用できます 。円の中に直角三角形を見つけて弦の長さを求めたり、空間で対角線の長さを計算したりと、幅広い問題で活躍します。

ポイントは「直角三角形を探す・作る」ことです。図の中に隠れた直角や補助線で作れる直角三角形を見抜けると、三平方の定理を使える場面がぐっと増えます。

まとめ

中学校で習う代表的な数学の公式の一つである「三平方の定理」。これは数学のなかでもとても実用性が高く、今後も座標平面での距離計算や図形の証明など様々な場面で登場します。今回学んだことを繰り返し練習して、ぜひ自分のものにしてください。

分からなくなったら基本に立ち返り、「a²+b²=c²」というシンプルな原点に戻って考えましょう。

三平方の定理を使いこなせるようになれば、直角三角形の問題はもう怖くありません！ぜひこの記事を活用して、三平方の定理マスターになりましょう！