【数学Ⅱ】指数関数をわかりやすく解説!計算方法やグラフ、公式の入門講座

「指数関数って、どういう意味?」そのような疑問を感じていませんか?
指数関数とは、簡単に言えば「数がどんどん増えていく」様子を表す関数です。
指数関数は、高校数学の中でも「わかりにくい」「グラフが急に伸びるのが怖い」と感じる生徒が多い単元です。しかし、定義とグラフの形をイメージでつかめば、グッと理解しやすくなります。
この記事では、「指数関数とはなにか」の定義から「基本的な計算方法」「グラフの読み方」「つまずきやすいポイント」「定期テスト対策につながる練習問題」までを紹介。
高校2年生のときに数学オリンピック本選に出場し、学習塾に通わずに東大へ現役合格した永田耕作さん(現在はカルぺ・ディエムで講演活動を実施)監修のもとで、指数関数の意味と定義、考え方を、図や具体例を使ってわかりやすく解説します。
永田先生
指数関数という名前を聞いてもピンと来ない人も多いでしょう。何のことだかさっぱりわからない人も。
ですが、関数の定義やイメージから問題の解き方まで、丁寧に解説していくので、何も心配は要りません。理解するまでじっくり追っていきましょう!
編集部
塾選ジャーナル編集部
塾選ジャーナル編集部です。『塾選ジャーナル』は、日本最大級の塾検索サイト『塾選(ジュクセン)』が提供する、教育・受験に関する総合メディアです。保護者が知っておきたい受験や進路情報をお届けします。
監修者
永田耕作
2001年生まれ 東京大学教育学部卒 公立高校から学習塾に入らずに東大へ現役合格。中学・高校は野球部に所属、部活動と勉強を並行し 「練習で自分の苦手を潰して、試合で自分の力を最大限に発揮する準備をする」という努力の「型」を 勉強にも活かして受験勉強を乗り切る。得意科目は数学で、高校2年生のときに数学オリンピック本選に出場した経験がある。現在は(株)カルぺ・ディエムに所属し全国各地で年間100回以上の講演活動を行い、勉強モチベーションや計画の立て方などを伝えている。自著に、「東大生の考え型(2022,日本能率協会マネジメントセンター)」「東大式 数値化の強化書(2024,彩図社)」などがある。 X公式アカウント:https://twitter.com/nagatakosaku08

目次
指数関数とは?意味・定義を高校生向けにやさしく解説

指数関数とは、簡単に言えば「数がどんどん増えていく」様子を表す関数です。「グラフが急に伸びるのが怖い」と感じることが多いのは、これが原因ですね。
例えば、「1日ごとに2倍になるウイルス」や「1年で1.05倍になる預金」など、一定の割合で増え方が加速する現象を表すときに使います。
数学では、指数関数は次のような形の式で表されます。
指数関数の定義「y = a^x」の形を覚えよう

指数関数の基本形は、y = a^x(aのx乗)です。この式で使われている文字の意味は次の通りです。
| 記号 | 意味 |
|---|---|
| y | 出力(結果) |
| a | 定数(aは0より大きく、1ではない) |
| x | 入力(変数) |
例えば、
- a=2 のとき: y = 2^x → 「xが1増えるたびに2倍」
- a=3 のとき: y = 3^x → 「xが1増えるたびに3倍」
xが1、2、3…と増えるとき、yは2、4、8、16…のように「かけ算」で増えます!これが、一次関数(+で増える)との大きな違いです。
永田先生
「指数関数」や「a^x」と聞いて難しく感じるかもしれませんが、決してそんなことはありません。
この
「指数」と「累乗」の違いってなに?
「指数関数」と聞くと、よく出てくるのが「指数って何?」「累乗とどう違うの?」という疑問です。実は、意味はほとんど同じですが、使い方に少しだけ違いがあります。
「指数」はかける回数を表す名前で、「累乗」は計算の結果を指します。

例えば、2³(2の3乗) という式があったとします。
このとき、上に小さく書かれた「³(3)」の部分を 「指数」 と呼びます。これは、「2を何回かけるか」 を表しています。
実際に 2×2×2 を計算すると、答えは 「8」 になります。この 計算そのものや、出てきた結果 のことを 「累乗」 といいます。
つまり、
- 「指数」はかける回数を表す名前
- 「累乗」はかけ算をした結果
という違いです。
永田先生
以上のように、「指数」はかける回数を説明するための言葉で、「累乗」は実際にかけた計算結果を意味しています。似たような言葉で混同しやすいですが、実際、意味は近いので、「違い」に神経質になりすぎなくても大丈夫です。
解答を書くときにどちらの言葉を使うかは、その度注意するようにして、経験から少しずつ覚えていきましょう。
指数関数の「a」に決まりがあるのはなぜ?(a > 0, a ≠ 1)
指数関数の形はy = a^xです。実はこの「a」には決まりがあります。
a > 0(0より大きい)、a ≠ 1(1ではない)
「なんでそんな決まりがあるの?」と思うかもしれません。
でも、これにはちゃんとした理由があります。
【理由1】a が 1 だと、どんな x でも y = 1 になる!
例えば、y = 1^x の場合、x が 0 や 100 、−50 でもすべて 1^x = 1 です。
つまり、グラフは横一直線となります。これでは「変化を示す関数」としての意味がなくなってしまいます。
【理由2】a が 0 以下だと、計算できないことがある!
例えば、a = −2 のときに x = 1/2 を代入すると(−2)^(1/2) = √(−2) となり、計算できません(※虚数になります)。
つまり、高校数学の範囲で扱う実数の世界では、計算できない x が出てきてしまうのです。
永田先生
「aは正の数で1以外」というルールは、見た目の美しさを重視して設けたわけではなく、「数学的に意味がある関数」として指数関数を統一するためのものです。
指数関数を上述の「かけ算で増える関数」として扱うための必須条件なので、必ず覚えましょう。
指数関数のグラフを図解で理解しよう

a > 1 のとき 指数関数はどう増える?
指数関数 y = a^x の「a」が 1より大きいとき(a > 1)、グラフはどうなるでしょうか?
答えは右に行くほど「一気に」大きくなるグラフになります。
例えば、a = 2 の場合を見てみましょう。
| x | y = 2^x |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
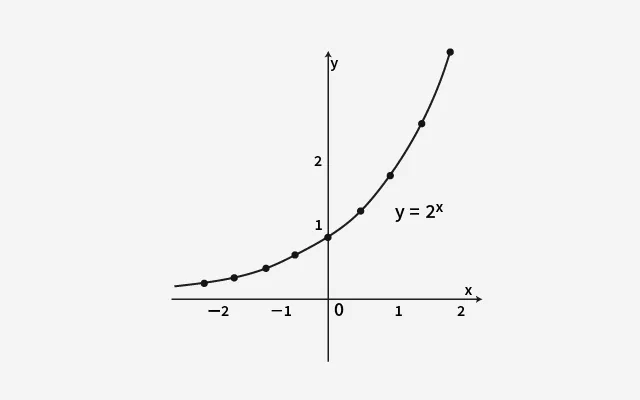
グラフを見ると、以下の3つの特徴がわかります。
- xが1増えるごとに、yが「倍々」で増える
- 最初はゆるやかだけど、急にグイッと上にのびる
- y軸の左(x < 0)では、値は 0に近づくけど0にはならない
このグラフの形は「指数関数の基本形」です。aが大きくなるほど、上に急カーブで伸びるイメージです。
永田先生
「倍々ゲーム」のように、指数関数ではxが小さいときはゆっくりと、そしてxが大きくなるにつれて一気にyの値が伸びていきます。
グラフの形を見るとそれが一目瞭然のはずです。
a < 1 のとき 指数関数はどう減る?
今度は、指数関数 y = a^x の「a」が 1より小さいとき(0 < a < 1) のグラフを見てみましょう。
例えば、a = 1/2(= 0.5)のとき
| x | y = 0.5^x |
|---|---|
| 0 | 1 |
| 1 | 0.5 |
| 2 | 0.25 |
| 3 | 0.125 |
| 4 | 0.0625 |
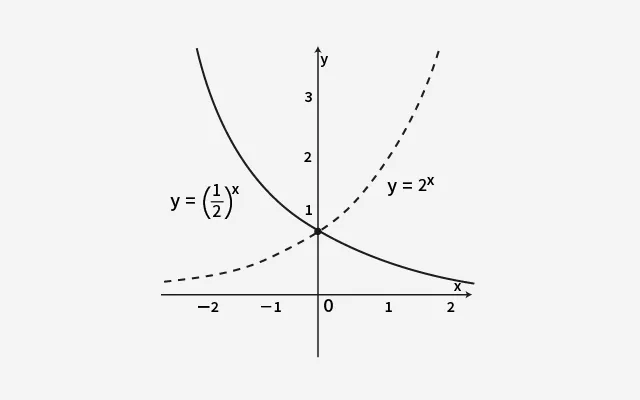
グラフを見ると、以下の3つの特徴がわかります。
- xが1増えるごとに、yが「半分ずつ」減っていく
- グラフは 右に行くほどゆるやかに下がり、0に近づく
- でも、0にはならない!
「a > 1」のときは「右上がりの急カーブ」、「a < 1」のときは「右下がりのゆるやかカーブ」
形は反対ですが、どちらも指数関数です。
永田先生
指数関数はaが1より大きければ「xに伴ってyが増える関数」ですが、1より小さくなると転じて「xに伴ってyが減る関数」になります。
また、y=0になることはないですが、0に限りなく近づいていく(これを漸近する、と言います)ことも重要なポイントです。グラフをよく見て特徴を頭に入れておきましょう。
xがマイナスのときグラフはどうなる?
指数関数 y = a^x において、xがマイナスの値(例:−1、−2など) のとき、グラフはどうなるのでしょう?
例えば、a = 2 の場合を見てみましょう。
| x | y = 2^x |
|---|---|
| −2 | 1/4 = 0.25 |
| −1 | 1/2 = 0.5 |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |

グラフを見ると、以下の3つの特徴がわかります。
- x が負になると、「a^x」は1より小さくなる
- x が小さくなる(左に行く)ほど、y の値はどんどん小さくなる
- ただし、y が 0 になることはない!
つまり、x がマイナスのとき、指数関数は「小さくなっていく」方向に伸びます。これは、a < 1 のグラフの右側の動きとよく似ています。
永田先生
xが負になると、指数関数の値は0と1の間の数になります。xが小さくなるにつれて(グラフで言うと左向きに進むにつれて)、yの値はどんどん小さくなっていきますが、決して0になることはありません。
この「限りなく0に近づく(漸近する)けれど0にはならない」という動きが、指数関数らしいところと言えます。
指数関数と一次関数・対数関数のグラフを比較しよう
指数関数をしっかり理解するには、他の関数と比べることがの近道です。
ここでは、以下の3つの関数のグラフを見比べてみましょう
| 関数の種類 | 式の例 | 特徴 |
|---|---|---|
| 一次関数 | y = x | 直線。増え方は「同じペース」 |
| 指数関数 | y = 2^x | カーブ。増え方が「だんだん速く」 |
| 対数関数 | y = log₂(x) | ゆるいカーブ。増え方が「だんだん遅く」 |
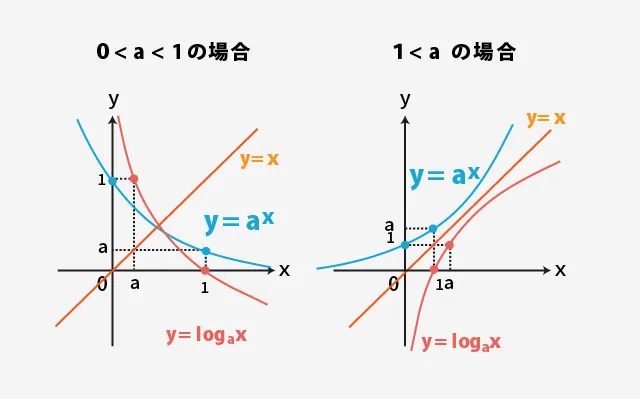
それぞれのグラフの特徴を見ると、以下のようになっています。
- 一次関数(y = x):x が1増えると、y も1増える→ 増え方はずっと一定(直線)
- 指数関数(y = 2^x):x が1増えると、yは2倍、4倍…と爆速で増える→ 最初ゆるやか → ある地点から急カーブ!
- 対数関数(y = log₂(x)):x が増えても、y はすこしずつしか増えない→ 右に行くほどゆるやかになるグラフ
グラフで見ると、この3つはまったく違う成長のスピードを持っています。
永田先生
これらの関数の違いは、「xの増加に伴うyの増え方」に注目すればすぐに見えてきます。
指数関数ははじめのうちは地味ですが、途中から他の関数を一気に追い抜いていく「遅咲きの成長タイプ」です。
高校生がつまずきやすい指数関数のポイントと対策

「なんでいきなり増えるの?」指数関数のイメージをつかむコツ
指数関数 y = a^x のグラフを見て、「なんで急にビュンッ!て伸びるの?」と思ったことはありませんか?
これは、指数関数が最初はあまり変化せず、後から急に伸びる「かけ算の世界」だからです。
一次関数と“増え方”を比べてみると、以下のようになります。
- 一次関数(y = 2x) → 「+2ずつ」増える(一定)
- 指数関数(y = 2^x) → 「×2ずつ」増える(どんどん速く)
| x | y = 2x | y = 2^x |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 2 | 2 |
| 2 | 4 | 4 |
| 3 | 6 | 8 |
| 4 | 8 | 16 |
| 5 | 10 | 32 |
→ 最初は同じくらいですが、x = 4 くらいから一気に追い抜くことがわかります。
永田先生
指数関数は「かけ算が何回続くか」でyの値が決まる関数です。最初は地味でも、少しxが大きくなれば、「止まらない成長」が見えるようになります。
これが指数関数の重要な特徴です。しっかり押さえておきましょう。
指数法則と指数関数の違い、混同していない?
「指数関数って、あの指数のルールのこと?」そう思っている人は、実はけっこう多いです。
しかし
- 指数関数:グラフで見る「関数(式)」のこと
- 指数法則:式の「計算ルール」のこと
→ まったくの別物! です。
「指数法則」ってなに?
指数法則とは、a^m × a^n = a^(m+n) のように、指数を使った計算のルールのことです。

「指数関数」は?
指数関数とは、y = a^x のように、変数(x)が指数にある関数のことです。つまり、「関数の種類」です。
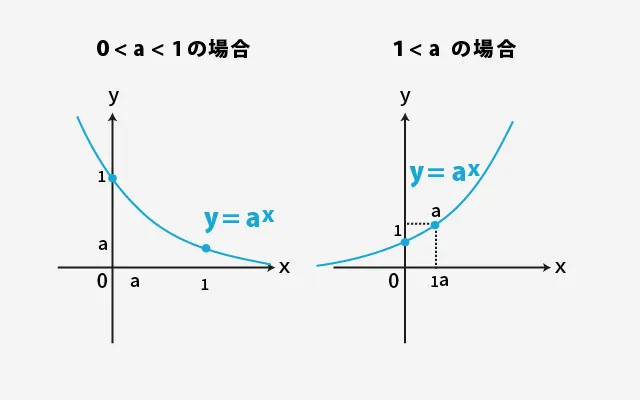
まとめると、以下のようになります。
| 用語 | 何を扱う? | 例 | 内容 |
|---|---|---|---|
| 指数法則 | 式の計算のルール | a² × a³ = a⁵ | 指数を使った「計算の仕方」 |
| 指数関数 | 数の変化・グラフ | y = 2^x | x が増えると y が倍々に増える関数 |
永田先生
指数法則は「計算ルール」のこと。一方で、指数関数は「数の動き」を表す「関数」です。
名前が似ていますが、まったくの別物。混同しないように注意しましょう!
計算でつまづきがちなパターンを解説
指数関数の計算は、式がシンプルに見えても、わずかな“見落とし”で間違いやすいところがたくさんあります。
ここでは、高校生がよくつまずく代表的なミスのパターンと、その対策を紹介します。
パターン1:a^x × a^y を「a^(x×y)」にしてしまう
例)a³ × a² をa⁵ではなく、a^3 × a^2 = a^6 にしてしまうミス!
正しくは「指数を足す」= a^(x + y)→ a³ × a² = a⁵ が正解!
パターン2:a^x ÷ a^y を「a^(x ÷ y)」と解釈してしまう
例)a⁶ ÷ a² をa^4ではなく、a^(6 ÷ 2) = a³にしてしまうミス!
正しくは「指数を引く」= a^(x − y)→a⁶ ÷ a² a^4となります。
パターン3:a^0 = 1 を忘れる/a = 0 でも使ってしまう
例)3^0 = 0としてしまう → 正しくは3^0 = 1
a ≠ 0 なら、a^0 = 1 は常に成り立つ!
パターン4:負の指数が出てくると焦ってしまう
例)2^−3 = −8としてしまう
負の指数は「逆数になる」と考える!→ 2^−3 = 1 / (2³) = ⅛
公式を覚えるだけでなく「使いどころ」を一緒に押さえるのが最大のポイントです。間違いの「あるある」を先に知っておくことで、ミスを回避しやすくなります。
永田先生
公式を忘れてしまったときやわからなくなってしまったとき、実際に具体的な数字を入れて計算して確認してみるとミスに気づきやすくなります。
例えば、a^x×a^yを計算しなければならないとき、a^(x•y)だと勘違いしていたとしても、実際にa=2、x=2、y=3などの数字を入れて計算してみると、2^2+2^3=12で、2^(2•3)=64とは異なる結果になるため、間違えていることに気づけます。
計算しやすい数を当てはめてみるとミスを防ぐことができるはずです。
定期テスト対策!指数関数のよく出る問題
問題1:指数法則の基本計算
次の式を簡単にしなさい。
(1) 2³ × 2²
(2) (3²)⁴
(3) 5⁰ × 5⁻²
(4) 4⁻¹ ÷ 4⁻³
問題2:指数関数のグラフ
次の関数のグラフについて答えなさい。
(1) y = 2^x のグラフは、次のうちどの特徴をもつか。
ア:右下がりの直線 イ:右上がりの曲線 ウ:x 軸と平行な直線
(2) y = (1/3)^x のグラフが必ず通る点を選びなさい。
ア:(1, 1) イ:(0, 1) ウ:(−1, 0)
問題3:変域の計算
関数 y = 2^x において、x の値が −2 から 3 のとき、y の変域を求めなさい。
定期テスト対策!指数関数のよく出る問題【解説編】
問題1:指数法則の基本計算
(1) 2³ × 2²
→ 2^(3+2) = 2⁵ = 32
※指数が同じ底のときは、指数を足す。
(2) (3²)⁴
→ 3^(2×4) = 3⁸ = 6561
※累乗の累乗は指数を掛ける。
(3) 5⁰ × 5⁻²
→ 1 × 1/25 = 1/25
※a⁰ = 1、負の指数は逆数になる。
(4) 4⁻¹ ÷ 4⁻³
→ 4^(−1 − (−3)) = 4² = 16
※割り算のときは指数を引き算する。
問題2:指数関数のグラフ
(1) y = 2^x のグラフの特徴:
→ 答え:イ:右上がりの曲線
※a > 1 の指数関数は、右肩上がりのカーブになる。
(2) y = (1/3)^x が通る点:
→ 答え:イ:(0, 1)
※どんな指数関数でも、x = 0 のときは y = 1 になる。
問題3:変域の計算
x が −2 から 3 のとき、y = 2^x
x = −2 → y = 1/4
x = 3 → y = 8
→ 答え:1/4 ≤ y ≤ 8
※与えられた x の範囲に対応する最小・最大の y を求める。
指数関数についてよくある質問(FAQ)

ここでは、指数関数についてよくある質問を解説します。
指数関数に登場する「e」とはどういう意味ですか?
指数関数の勉強を進めると、「e」という文字が登場する式を見ることがあります。例えば、y = e^x という形です。この「e」は、定数であり、数学の中でも特に重要な値のひとつです。
e は「自然対数の底」と呼ばれるもので、およそ 2.718 という値を持っています。円周率 π(パイ)のように、正確な値は小数がずっと続く無理数です。
では、なぜ e を使うのでしょうか?それは、e^x という指数関数が、自然現象や経済、微分・積分など多くの分野で非常に扱いやすい性質を持っているからです。例えば、y = e^x の微分は、そのまま y = e^x になります。つまり「あるxにおけるyの値とそのグラフの傾きの値が常に等しい関数」という特別な性質があるのです。
微分公式
高校数学では、数III(数学Ⅲ)で本格的に学習しますが、定期テストレベルでは「e は特別な定数であり、約2.7くらい」として押さえておけば十分です。理系に進む人や、より発展的な数学に触れる際には、必ず重要になる概念です。
永田先生
数学に苦手意識がある人は「eは2.7くらいの特別な数」という認識を持っておけば大丈夫です。
数Ⅲでしっかり習うので、はじめのうちはeを見たらひとまず「定数」であることだけ意識してください。
指数関数と対数関数、どう違いますか?
どちらも「a^x」という形に関係しますが、役割がまったく違います。
| 関数 | やっていること | 例 |
|---|---|---|
| 指数関数 | 「xを使って、a^x を計算する」 | x = 3 → 2³ = 8 |
| 対数関数 | 「a^x = y を満たす x を探す」 | 2^x = 8 → x = 3 |
つまり、対数関数は指数関数の“逆”をしてくれる関数です!
例えば、「最初に1つあったウイルスが、1日ごとに2倍になるとしたら、何日後にいくつになるか?」→ これは対数関数で考える場面です。
今度は逆に、「いまウイルスが128個あるけど、2倍ずつ増えてきたとしたら、何日前は1個だった?」→ これは対数関数で考える場面です。
やっていることは「いつ増え始めたか?」を逆にたどっているだけ。増えるスピードの逆算”をしている関数です。
永田先生
指数関数と対数関数は表裏一体です。どちらも「倍々の世界」を扱いますが、前に進むのか、後ろにさかのぼるのか、という違いがあります。
対になっている概念なので、セットで理解すると定着しやすいでしょう。
指数関数は何に使われますか?将来の役に立ちますか?
「こんな関数、テストだけの話でしょ?」「どうせ実生活で使わないし……」そう思ってしまう気持ち、よくわかります。でも、実は指数関数は現実のいろんな場面で使われています!
身近なところでの活躍例
- ① ウイルスの感染拡大(※コロナ禍で話題に)
- ② 銀行の利息や投資(複利)
- ③放射性物質の減り方や細胞分裂など、科学や自然の現象
- ④地震のマグニチュードの計算
- ⑤ネズミ算(1人が3人に紹介して、また3人ずつ……といった形の計算)
つまり、指数関数は「ものごとがどんどん速く変わっていくとき」に現実を説明する“モデル”として使われています!
永田先生
指数関数は「ゆるやかに始まって、だんだんと急に変わるようになっていく現象を表す関数」です。
社会・科学・お金の世界など、あらゆる分野で使うので、どの道に進むにしろ、覚えておいて損はありません。
指数関数は高校何年生で学習しますか?
指数関数は、高校2年生で学ぶ「数学Ⅱ」の単元のひとつです。文系・理系どちらの生徒も学ぶ内容で、共通テストにもよく出題されます。
ただし、理系ではより深く扱う(グラフの変化・微分・eなど)ため、後半で発展的な内容に進みます。
「指数関数的に増える」とはどういう意味ですか?
「指数関数的に増える」とは、時間がたつにつれて、ものすごい速さで増えていくことを意味します。
例えば、最初は1ずつしか増えないように見えても、次第に2倍、4倍、8倍…と、倍々のペースで増えていくのが指数関数的な増え方です。
これは y = a^x(a > 1)のような指数関数の特徴であり、人口の増加、ウイルスの感染拡大、インターネットのデータ量など、実際の社会現象でもよく見られます。
「急に増える」「後から一気に跳ね上がる」というイメージを持っておくと理解しやすくなります。
永田先生
一次関数が「マラソン」なら、指数関数の伸び方は「ロケット」に例えることができるでしょう。「指数関数的に増える」とは、数そのものだけでなく、その数が増えるスピードまでもが加速していくということを意味します。
これが一次関数とは違う「怖さ」と「すごさ」なのです。
指数関数を電卓で計算するときは?
数学の問題で出てくる「指数関数の値」は、電卓で計算できます。多くのスマホや関数電卓には、以下のような「指数計算」用のボタンがあります。
| 意味 | 押すボタンの順番(例) | |
|---|---|---|
| ^ や y^x | 指数(べき乗)を計算する | 2 → ^ → 3 → = → 8 |
| e^x | e を使った指数関数(eの何乗) | e^x → 2 → = → 約7.389 |
数学は塾に通って対策すべきですか?
数学が苦手、あるいは少しでも不安があるなら、塾に通って学習することは有効な選択肢です。
とくに指数関数のような抽象的な単元は、教科書や学校の授業だけでは理解しづらいこともあります。塾では、わかりやすい図や具体的な例を使って丁寧に説明してくれるため、つまずきやすい内容も整理して学べます。
また、塾では定期テストや入試を意識した演習をくり返すことで、知識の定着が早くなります。学校では時間をかけにくい「個別の弱点対策」や「解き方のコツ」なども、塾なら自分のペースで学べる点が強みです。
もちろん、自学自習で十分に理解できる人もいますが、継続して成績を上げたい人、数学に少しでも不安がある人にとっては、塾に通うことで大きな安心と自信につながるでしょう。
まずは体験授業や無料相談などを利用して、自分に合うかどうかを試してみるのもひとつの方法です。
まとめ 指数関数は「考え方」でわかる!

指数関数は、見た目が難しそうな数式でも、「倍々に増える」「どんどん加速する」というイメージをつかむだけで、グッと理解しやすくなります。
- 指数関数とは? → 「y = a^x」の形。“増え方のスピード”を見る関数
- a の条件ってなに? → a > 0、a ≠ 1 → グラフが意味を持つための大事なルー
- グラフの形を見れば、動きがわかる! → a > 1 なら「急にグンッと上に伸びる」カーブ
- 指数法則と指数関数は別物! → 「計算のルール」と「関数の種類」、ちゃんと区別しよう
- 身の回りでも使われている!→ ウイルス・投資・SNSなど…指数関数は“現実の変化”にぴったり
指数関数は、文系・理系どちらに進んでも避けて通れない単元です。しかし「苦手だ」と思う前に、まずはどういう考え方で動いているのかをつかんでみましょう。式を丸暗記するより、「あ、こういう動きをするんだな」と感覚で理解することが近道です!
指数関数は「スピードの変化」を見る数学です。暗記するのではなく、感覚で理解するほうが楽に得点につながります。
執筆者プロフィール

塾選ジャーナル編集部です。『塾選ジャーナル』は、日本最大級の塾検索サイト『塾選(ジュクセン)』が提供する、教育・受験に関する総合メディアです。保護者が知っておきたい受験や進路情報をお届けします。
監修者プロフィール

2001年生まれ 東京大学教育学部卒 公立高校から学習塾に入らずに東大へ現役合格。中学・高校は野球部に所属、部活動と勉強を並行し 「練習で自分の苦手を潰して、試合で自分の力を最大限に発揮する準備をする」という努力の「型」を 勉強にも活かして受験勉強を乗り切る。得意科目は数学で、高校2年生のときに数学オリンピック本選に出場した経験がある。現在は(株)カルぺ・ディエムに所属し全国各地で年間100回以上の講演活動を行い、勉強モチベーションや計画の立て方などを伝えている。自著に、「東大生の考え型(2022,日本能率協会マネジメントセンター)」「東大式 数値化の強化書(2024,彩図社)」などがある。 X公式アカウント:https://twitter.com/nagatakosaku08











