【数学Ⅱ】対数関数とは?基本公式やグラフ、計算方法をイチから解説

「対数関数って、何のためにあるの?」高校数学で急に出てくる「対数関数」に、戸惑っている人も多いのではないでしょうか。でも実は、対数関数は指数関数の逆の考え方をするだけの、とてもシンプルな仕組みです。
対数とは、そもそも、「ある数(底)を何回かければ、ある数(真数)になるか」を表したもの。対数関数とは、その対数を求める関数です。
この記事では、高校2年生のときに数学オリンピック本選に出場、学習塾に入らずに東大へ現役合格し、現在はカルぺ・ディエムでさまざまな講演活動をおこなっている永田耕作さん監修のもと、対数関数の意味・定義・考え方を、図や具体例を使ってわかりやすく解説します。数学が苦手な人でも基礎から理解できる内容です。
編集部
塾選ジャーナル編集部
塾選ジャーナル編集部です。『塾選ジャーナル』は、日本最大級の塾検索サイト『塾選(ジュクセン)』が提供する、教育・受験に関する総合メディアです。保護者が知っておきたい受験や進路情報をお届けします。
監修者
永田耕作
2001年生まれ 東京大学教育学部卒 公立高校から学習塾に入らずに東大へ現役合格。中学・高校は野球部に所属、部活動と勉強を並行し 「練習で自分の苦手を潰して、試合で自分の力を最大限に発揮する準備をする」という努力の「型」を 勉強にも活かして受験勉強を乗り切る。得意科目は数学で、高校2年生のときに数学オリンピック本選に出場した経験がある。現在は(株)カルぺ・ディエムに所属し全国各地で年間100回以上の講演活動を行い、勉強モチベーションや計画の立て方などを伝えている。自著に、「東大生の考え型(2022,日本能率協会マネジメントセンター)」「東大式 数値化の強化書(2024,彩図社)」などがある。 X公式アカウント:https://twitter.com/nagatakosaku08

目次
対数関数とは?意味・定義を高校生向けにやさしく解説

「対数関数」という言葉を聞いて、難しそうと感じる人も多いでしょう。しかし対数関数は、すでに学んだ指数関数と逆の関係にある、理解しやすい関数です。
対数とは、「ある数(底)を何回かけると、目的の数(真数)になるか」を表す考え方です。対数関数は、その回数を求めるための関数のことをいいます。
基本的な形は、以下の通りです。
log_b(a) = c
これは、「b を何回かけると a になるか?」を表しており、その答えが c です。
対数関数は、y = logax (a>0, a≠1) の形で表されます。ここでは、数式が苦手な人でもわかるように、対数の考え方を基本からやさしく解説します。
指数関数と対数関数は「逆」の関係
対数関数を理解するうえで、最も大事なポイントは「指数関数との関係」です。対数関数は指数関数の「逆」のはたらきをする関数です。
例えば、次のような指数の式を考えてみましょう。
2の3乗は8です。つまり、2 × 2 × 2 = 8となります。

これは「2を3回かけると8になる」という意味です。では、この式を逆の立場から見てみましょう。
「2を何回かければ8になるか?」と考えると、答は「3」です。このときに使うのが、対数(log)です。
log₂(8) = 3
この式は、「8は2を何回かけた数か?」という問いの答えが3であることを表しています。
指数関数と対数関数の関係を表にまとめると、以下のようになります。
| 種類 | 式の例 | 意味 |
| 指数関数 | 2^3 = 8 | 2を3回かけると8になる |
| 対数関数 | log₂(8) = 3 | 2を何乗すれば8になるか → 答えは3 |
永田先生
指数と対数は表裏一体の関係にあります。指数関数が「かける」動きを示すなら、対数関数はそれを「さかのぼる」動きを示すものです。まずはこの「逆の関係」という感覚を持つと理解しやすくなるでしょう。
対数の表記に使う「log」や「底」とは?用語を解説
数学の対数関数では、「log(ログ)」という記号を使います。これは「logarithm(対数)」の略で、ある数を何回かければ目的の数になるかを表します。
logの意味
例えば、次のような式があります。
log₂8 = 3
これは、「2を何回かけたら8になるか?」ということを式で表したものです。実際に、2 × 2 × 2 = 8 なので、答えは3です。
このように、logは「指数を求める」ための記号として使用されます。
「底(てい)」の意味
logの右下に書かれている数を底(てい)といいます。底は、何を何回かけるのかを示す基準の数です。
例えば、
- log₂(8) の底は 2
- log₁₀(1000) の底は 10
底が変わると、何乗すればよいかの考え方も変わります。
なお、「log(x)」と底が省略されている場合は、慣習として「底が10」と決められています。
例えば、log(100)は底が10と考えるのでlog(100) は log₁₀(100) となります。
logに使える数の条件
対数の式log(x)では、かっこの中に入る数は、0より大きい正の数に限られます。
つまり、次のような式は意味を持ちません。
- log(0)
- log(-2)
これは「何乗したら0になるか」や「何乗したら負の数になるか」は、通常の対数では答えが出せないためです。そのため、対数関数のグラフは x > 0 の範囲でしか描けません。
対数の式の構成を確認しよう
対数の基本的な形は、以下の通りです。
log_b(a) = c
これは、「b を何回かければ a になるか?」を表しており、その答えが c です。
例えば、log₂(8) = 3 の場合:
- 底(b)… 2
- 真数(a)… 8
- 答え(c)… 3
このように、対数の式には「底」「真数」「指数」という3つの要素があります。
永田先生
見慣れない記号や初めて知った概念でも、指数関数の知識と結びつけて考えれば、自然と理解できるはずです。
覚えておきたい対数の性質3つ
対数関数を学ぶうえで、これだけは押さえておきたい基本の性質が3つあります。
すべて覚えようとすると難しく感じますが、まずは次の性質をしっかり理解しましょう。
底は「0より大きく1ではない実数」
対数で使う底(てい)にはルールがあります。
底は、次のような2つの条件を満たす実数でなければなりません。
- 0より大きい(正の数)
- 1ではない
具体例
- OK → 2、10など
- NG → 0、1、−3 など
底が1だと、どの真数に対しても対数の値が同じになり、数学的に意味のある関数として成り立たなくなります。
真数が1のとき、対数は必ず0
対数の式で真数(括弧の中の数)が1のときは、必ず結果が0になります。
理由は、どんな数でも0乗すると1になるるからです。
このため、「真数が1なら対数は0」と覚えておきましょう。
真数が底と同じ実数のとき、対数は必ず1
真数が底と同じときは、答えは必ず「1」になります。
理由はとてもシンプルで、どんな数でも1乗すればその数になるからです。
例:
- log₂(2) = 1(2を1回かけると2)
- log₁₀(10) = 1(10を1回かけると10)
- log₃(3) = 1(3を1回かけると3)
指数の意味を思い出せば、この性質はすぐに理解できます。
| 式 | 結果 | 理由 |
|---|---|---|
| log₂(1) | 0 | 2の0乗は1 |
| log₁₀(10) | 1 | 10の1乗は10 |
| log₅(1) | 0 | 5の0乗は1 |
| log₃(3) | 1 | 3の1乗は3 |
- 底は0より大きく、1ではない
- 真数が1なら対数は0
- 真数と底が同じなら対数は1
これらは、対数を使った問題を解くときに頻繁に登場します。まずはこの3つの性質を暗記しておくことが、対数理解の第一歩です。
永田先生
これら3つの性質を理解した上でしっかり覚えておくと、対数の基本問題はスムーズに解けるようになります。まずは、式を見たときに「これはゼロになるやつだな」と反射的に求められるようになることを目指しましょう。
これだけは覚えたい!対数の基本公式
対数にはいくつかの便利な公式があります。そのなかでも、基本的で頻出な公式はしっかりと押さえておきましょう。
対数の積の公式
対数の積に関する公式は、次の通りです。
log_b(x × y) = log_b(x) + log_b(y)
意味:「xとyをかけた数の対数は、それぞれの対数を足したものと等しい」

例えば、次のような計算を考えます。
log₁₀(100 × 1000)
これは、100と1000をかけた数の対数です。
実際に公式を使うと:
log₁₀(100) + log₁₀(1000) = 2 + 3 = 5
log₁₀(100,000) も 5 になるので、公式が正しいことが確認できます。
なぜこの公式が便利なのか?
この公式を使うと、「かけ算された数の対数」を、別々の数の対数に分解して計算できるようになります。
注意点
- この公式が使えるのは、両方の数(xとy)が正の数のときだけです。
- 底(b)が共通であることも前提条件です。
永田先生
対数の基本として、「かけ算が足し算になる」この公式をしっかり理解して、覚えておきましょう。たまに真数同士の足し算を対数の足し算に分解してしまうミスを見かけますが、わからなくなった時は対数関数の本来の定義に立ち返って考えてみるとミスを防ぐことができます。
対数の商の公式
「商(わり算)」に関する対数の公式は、割り算された数の対数を、引き算として計算できる便利な公式です。
対数の商の公式
log_b(x ÷ y) = log_b(x) − log_b(y)
意味: 「xをyで割った数の対数は、xの対数からyの対数を引いたものと等しい」

具体例で理解しよう
次のような計算を考えてみましょう。
log₁₀(1000 ÷ 10)
この場合、1000 ÷ 10 = 100 なので、
log₁₀(1000 ÷ 10) = log₁₀(1000) − log₁₀(10)= 3 − 1= 2 と表せます。
log₁₀(100) = 2 なので、公式が正しいことがわかります。
なぜこの公式が便利なのか?
かけ算のときと同様に、複雑な割り算を、より簡単な引き算で処理できるのが大きなメリットです。
注意点
- 商の公式も、xとyの両方が正の数であることが前提です。
- 底(b)が同じであることも忘れずに確認しましょう。
永田先生
「割り算が引き算になる」というのは、対数の基本公式のなかでも非常に実用的なものです。複雑な計算でも、logの性質を知っておくだけで、スムーズにかつ正確に処理できるようになります。必ず押さえておきましょう。
対数の累乗の公式
累乗(るいじょう)とは、同じ数を何回もかけることです。対数関数では、累乗になっている数の対数をかけ算として処理できる便利な公式があります。
対数の累乗公式
log_bn = n × log_b(x)
※「xのn乗」は、xをn回かけたものです。
意味:「xのn乗の対数は、n倍のlog_b(x)になる」

具体例で理解しよう
例:log₁₀(1003) を計算してみましょう。
まず、1003 100 × 100 × 100 = 1,000,000 です。
log₁₀(1003) = log₁₀(1000000) = 6
一方、log₁₀(100) = 2 なので、
3 × log₁₀(100) = 3 × 2 = 6
どちらも同じ結果になることが確認できます。
このように、累乗された真数は、対数の前にかけ算として外に出すことができます。
公式の活用シーン
- 指数がついている計算を、かけ算に変えて簡単にする
- 対数のグラフを変形するときに使う
注意点
- x は正の数である必要があります。
- n は実数であればよく、整数でなくてもかまいません(ただし高校では自然数の範囲で考えることが多い)。
永田先生
この公式を使えば、指数のついた真数が出てきたとき、対数のかけ算に変えて計算しやすくすることができます。指数と対数の関係性がより深く見える場面と言えるでしょう。直感的に覚えておくと定着しやすいです。
底の変換公式
対数には「底(てい)」という数があります。logの右下に書かれるこの底は、公式を使う時にはそろっている必要があります。
しかし、現実の問題では「底が異なる対数」が出てくることもあります。そのようなときに使えるのが、底を別の数に変換する公式(底の変換公式)です。
底の変換公式の形
log_b(a) = log_c(a) ÷ log_c(b)
意味:「底bの対数は、別の底cを使った対数の比で表せる」

この公式を使えば、例えば底bの対数を、別の底c(たとえば10やeなど)の対数に変えられます。
具体例で理解しよう
例えば、log₂(8) を計算したいときを考えます。この公式を使えば、log₂(8)は次のように変換できます。
log₂(8) = log₁₀(8) ÷ log₁₀(2)
おおよその値に置きかえると:
log₁₀(8) ≒ 0.903、log₁₀(2) ≒ 0.301
よって、0.903 ÷ 0.301 ≒ 3
実際、2の3乗は8なので答えは正しいことがわかります。
永田先生
底の変換公式は一見複雑に見えますが、基本は「底をそろえるための道具」です。これを使えば先に進めないように見える計算でも、変形することができます。しっかりとマスターしましょう。
グラフで覚えよう!対数関数の特徴
対数関数は式だけでなく、グラフでイメージを持つことが大切です。
グラフを見れば、「どこで定義されていて、どんな動きをする関数なのか」が感覚的にわかります。
底aによってグラフの形が変わる
対数関数には、底という数があり、これが変わるとグラフの形も変わります。
一般的な対数関数は以下のように書かれます。
y = log_a(x)
ここでの a が「底」です。底によって、グラフの傾きや伸び方が変化します。
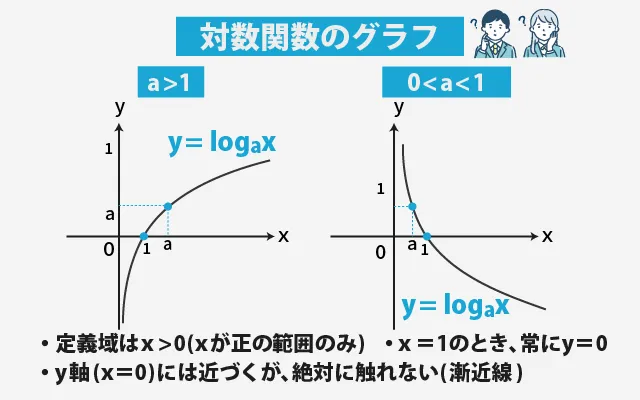
a > 1 のとき(底が1より大きい)
このとき、グラフは右上がりの曲線になります。
例:
- y = log₂(x)
- y = log₁₀(x)
特徴:
- xが大きくなると、yもゆっくり大きくなる
- x = 1 のとき y = 0(どんな底でも共通)
- x軸の左側(x ≦ 0)にはグラフが存在しない(定義されない)
0 < a < 1 のとき(底が1より小さい正の数)
このとき、グラフは右下がりの曲線になります。
例:
- y = log₀.₅(x)
特徴:
- xが大きくなると、yは小さくなる(負の方向へ)
- やはり x = 1 のとき y = 0
- グラフは「減少関数」となる
共通するポイント
- 定義域は x > 0(xが正の範囲のみ)
- x = 1 のとき、常に y = 0
- y軸(x = 0)には近づくが、絶対に触れない(漸近線)
永田先生
対数関数のグラフは式よりも形で理解するのが近道です。底によって右上がりか右下がりかが決まること、そしてどんな底でもx=1のときにy=0、すなわちx軸と交わることは必ず押さえておきましょう。
対数関数のグラフのポイント
対数関数のグラフは、最初は少しとっつきにくく見えるかもしれません。しかし、いくつかの共通するポイントを押さえるだけで、グラフの形をイメージできるようになります。
1. 定義域は「x > 0」
対数関数では、xが0以下の値になると計算できません。これは「何乗して0やマイナスの数になるか?」という問いに、答えが存在しないためです。
そのため、グラフはxが正の範囲(x > 0)にしか描かれません。
2. x = 1 のとき、必ず y = 0 を通る
どんな底aを使っても、x = 1 のときのyの値は必ず0になります。これは「aの何乗が1になるか?」という問いで、答えは必ず「0乗」になるからです。
例:
- log₂(1) = 0
- log₁₀(1) = 0
- log₀.₅(1) = 0
このように、グラフは必ず (1, 0) を通ります。
3. y軸には絶対に触れない
グラフは、xが0に近づくにつれて、yの値がマイナス無限大に向かって下がり続けます。
しかし、x = 0 には決して届かず、y軸に漸近(近づいていく)していく形になります。
これを「x = 0 は縦の漸近線になる」といいます。
4. 底の大きさで曲線の形が変わる
底aの値によって、グラフの傾きが変わります。
- a > 1 のとき…右上がりのグラフ(増加関数)
- 0 < a < 1 のとき…右下がりのグラフ(減少関数)
いずれも、先ほどの共通点(x > 0、x = 1 で y = 0、x軸の左側に描けない)は同じです。
永田先生
グラフは見て慣れるのが一番手っ取り早いです。定義を考えようとすると難しく感じるかもしれませんが、「x>0の範囲だけに存在する」「x=1のときy=0の点を必ず通る」「右上がりか右下がりかの2種類があり、それは底の値で決まる」の3点を押さえるだけで、スムーズに理解できます。
定期テスト対策!対数関数のよく出る問題
対数関数は、高校数学の定期テストでよく出題される分野のひとつです。公式を覚えるだけではなく、実際に使えるようになることがとても大切です。
ここでは、定期テストでよく登場する公式を実際に使ってマスターしていきましょう。
対数の積の公式の問題
まず、対数の積の公式をおさらいしましょう。
log_b(x × y) = log_b(x) + log_b(y)
この公式を使えば、かけ算の中にある数を足し算に変換して計算することができます。
例題 1:
次の値を公式を使って計算しなさい。
log₁₀(100 × 1000)
例題 2:
次の式を、logの足し算の形に変えなさい。
log₃(9x)
対数の商の公式の問題
対数の「商の公式」は、割り算を引き算に変える公式です。計算や式の変形問題でよく登場しますので、定期テスト前にはしっかり確認しておきましょう。
商の対数公式の基本形
log_b(x ÷ y) = log_b(x) − log_b(y)
意味:「xをyで割った数の対数は、xの対数からyの対数を引いたものと等しい」
例題 1:
次の値を計算しなさい。
log₁₀(1000 ÷ 10)
例題 2:
次の式を、logの引き算の形に変えなさい。
log₄(x ÷ 16)
対数の累乗の公式の問題
累乗に関する対数の公式は、指数がついた真数の対数を簡単に計算したいときにとても便利です。
テストでは「式の変形」や「値の計算」に使う場面がよく出てきます。
累乗の対数公式のおさらい
log_b(xのn乗) = n × log_b(x)
意味:「xのn乗の対数は、n倍の log_b(x) にできる」
例題 1:
次の値を計算しなさい。
log₁₀(100^3)
例題 2:
次の式を変形しなさい。
log₅(x^4)
底の変換公式の問題
底の変換公式は、logの底が変えられない状況で計算する必要があるときに使う便利な公式です。定期テストでは、「logの底が2や5など特別な値になっていて、そのまま計算できない」ときに登場します。
底の変換公式のおさらい
log_b(a) = log_c(a) ÷ log_c(b)
意味: 「底bの対数は、任意の底cを使った log の比で表すことができる」
※ 一般的には、c = 10(常用対数)などにすることが多いです。
例題 1:
次の値を、log₁₀を使って計算しなさい。
log₂(8)
例題 2:
次の式を、底10のlogを使った式に変形しなさい。
log₄(x)
定期テスト対策!対数関数のよく出る問題【解説編】
ここでは、定期テストに出やすい「対数関数の基本問題」を、実際の問題に即して、公式の使い方と計算の流れをていねいに解説していきます。
まずは「積の対数公式」を使った問題から確認しましょう。
積の対数公式の問題の解説
例題 1(基本)
次の値を公式を使って計算しなさい。
log₁₀(100 × 1000)
【解説】
100 × 1000 = 100000 なので、計算すると:
log₁₀(100 × 1000)= log₁₀(100) + log₁₀(1000)= 2 + 3= 5
例題 2(式の変形)
次の式を、logの足し算の形に変えなさい。
log₃(9x)
【解説】
1:「9」と「x」の積と考え、公式を使います。公式にあてはめると次のようになります。
log₃(9x) = log₃(9) + log₃(x)
2:log₃(9) を計算します。
32=9なのでlog₃(9)=2
3: したがって式は下記のようになります。
log₃(9x) = 2 + log₃(x)
よくある間違いと注意点
- log₃(x + y) は公式で分けられません。
「かけ算のときだけ分けられる」という点に注意が必要です。log₃(x + y) ≠ log₃(x) + log₃(y)(←これは間違い)
- 真数(logの中身)が正の数であることが前提です。
永田先生
「log(かけ算)はlogの足し算にできる」という変換のイメージをしっかりもちましょう。実際に計算して納得してから使ってみることが大事です。 計算ができるだけでなく、「変形の途中式」も書けるようになっておくと、テストで得点しやすいでしょう。
商の対数公式の問題の解説
例題 1(基本の計算)
次の値を計算しなさい。
log₁₀(1000 ÷ 10)
【解説】
まず、公式を使って分解します。
log₁₀(1000 ÷ 10) = log₁₀(1000) − log₁₀(10)= 3 − 1= 2
例題 2(式の変形)
次の式を、logの引き算の形に変えなさい。
log₄(x ÷ 16)
【解説】
log₄(x ÷ 16) = log₄(x) − log₄(16)
さらに、log₄(16) = 2(なぜなら 4の2乗 = 16)なので、
log₄(x) − log₄(16)= log₄(x) − 2
よくある間違いと注意点
- log_b(x − y) は変形できません!
引き算の中身を対数に分解することはできないので注意しましょう。× log₃(x − y) ≠ log₃(x) − log₃(y)(←これは誤り)
- 商の公式が使えるのは、「割り算」のときだけです。
- 真数(x, y)はどちらも正の数でなければなりません。
永田先生
「log(割り算)はlogの引き算に変えられる」この発想を何度も練習してしっかり身につけましょう。logの計算で引き算が出てきたら、商の形から変形したのかも? と逆に疑ってみることも大切です。
累乗の対数公式の問題の解説
例題 1(基本の計算)
次の値を計算しなさい。
log₁₀(100^3)
【解説】
100^3 は 100 × 100 × 100 = 1,000,000 なので
log₁₀(100^3) = 3 × log₁₀(100)
log₁₀(100) = 2(10の2乗が100)なので、
3 × 2 = 6
答え:6
例題 2(式の変形)
次の式を変形しなさい。
log₅(x^4)
【解説】
公式に従って、指数を前に出します。
log₅(x^4) = 4 × log₅(x)
この変形ができるだけで、式の計算や整理がずっと楽になります。
よくある間違いと注意点
- 「指数」だけが前に出せるということを意識しましょう。xがかけ算や足し算になっている場合には使えません。
- xが負の数や0の場合、この公式は使えません(logは真数が正の数でないと定義されない)。
永田先生
「底が何かの累乗になっていたとき、その指数は前に出せる」この操作に慣れておくと、一見難しそうな式もシンプルに整理することができます。「累乗→かけ算」という変形をする公式と覚えておくと、直感的に理解しやすいでしょう。
底の変換公式の問題の解説
例題 1(基本)
次の値を、log₁₀を使って計算しなさい。
log₂(8)
【解説】
log₂(8) = log₁₀(8) ÷ log₁₀(2)
電卓などを使うと:
- log₁₀(8) ≒ 0.903
- log₁₀(2) ≒ 0.301
よって、0.903 ÷ 0.301 = 3
これは、2の3乗が8であることからも確認できます。
例題 2(式の変形)
次の式を、底10のlogを使った式に変形しなさい。
log₄(x)
【解説】
log₄(x) = log₁₀(x) ÷ log₁₀(4)
よくある間違いと注意点
- 分母と分子の順番を間違えやすいので注意!
log_b(a) = log_c(a) ÷ log_c(b)(←正しい)
× log_c(b) ÷ log_c(a)(←これは間違い)
- 真数と底の順序をしっかり覚えておきましょう。「a が上、b が下(真数が分子、底が分母)」と覚えるとよいです。
永田先生
「底が異なるときは、分数にして共通の底にそろえる」という感覚を、演習を積むことで掴んでいきましょう。この公式は変換公式という名前の通り、底を変換して計算を先に進めてくれます。
対数関数についてよくある質問(FAQ)

ここでは、対数関数についてよくある質問を解説します。
指数関数と対数関数、どう違いますか?
対数関数は、指数関数の「逆」の関数です。
例えば、指数関数では「2の3乗は8(2 × 2 × 2 = 8)」のように、何乗するかを決めて、その結果を求めます。これを数式で書くと「2^3 = 8」です。
一方、対数関数では「2を何回かければ8になるか?」という逆の問いを立てます。このときの答えが3なので、「log₂(8) = 3」と書きます。
つまり、指数関数が「かける回数から結果を出す関数」なら、対数関数は「結果から、何回かけたかを求める関数」です。
どちらも同じ関係を別の方向から見ているだけなので、式の中で「入力と出力」が入れ替わったような関係になっています。
混乱しやすいポイントですが、「対数は指数をひっくり返したもの」と覚えると、わかりやすくなります。
対数関数は何に使われますか?将来の役に立ちますか?
対数関数は意外と身近なところで使われていて、将来も役立つ場面があります。
例えば、音の大きさを表す「デシベル(dB)」や、地震の強さ「マグニチュード」は、どちらも対数の考え方を使われています。
また、細菌の増殖や人口の増加など、変化の速いものをグラフにするときに、対数のスケールを使うと見やすくなることがあります。
高校ではイメージしにくいかもしれませんが、大学での自然科学・工学・経済学など、幅広い分野で対数が使用されます。
日常生活で直接使う機会は多くありません。しかし、将来、科学・IT・分析の分野に進む場合、対数の知識は有用です。
数学が苦手でも「対数=指数の逆」という基本的なイメージを持っておくことで、後に学び直す際に理解の助けとなるでしょう。
対数関数は高校何年生で学習しますか?
対数関数は、一般的には高校2年生で学習します。
対数関数は、数学IIの単元のひとつとして学習します。まず「指数関数」を学び、その次に「対数関数」を学ぶのが一般的です。。
数学Iではまだ扱われず、数学IIの中盤〜後半にかけて学習することが多いでしょう。。学校によって進度は異なりますが、2年生の1学期または2学期ごろに扱われるのが一般的です。
数式に慣れていないと最初はとっつきにくいかもしれませんが、「指数の逆」だとわかれば、理解しやすくなります。
対数でlog2の計算方法は?
直接 log₂(底が2)を計算することはできないケースが多いので、底の変換公式を使います。
log₂のような対数を計算するときは、底の変換公式を使って、常用対数に直すのが一般的です。
変換公式: log₂(x) = log₁₀(x) ÷ log₁₀(2)
例えば、log₂(8) を計算したい場合は、
log₂(8) = log₁₀(8) ÷ log₁₀(2)
≒ 0.903 ÷ 0.301
≒ 3
このようにして、 log₂ の値を求めることができます。
log10底の100の場合、いくつになりますか?
log₁₀(100) の値は 2 になります。
理由は、10を何乗したら100になるかを考えればすぐわかります。
10 × 10 = 100
つまり、10の2乗が100なので、
log₁₀(100) = 2
と求められます。
このように、log₁₀(x) は「10を何回かけたらxになるか」を表すものです。log₁₀(10) = 1、log₁₀(1000) = 3 なども同じ考え方で求められます。
数学は塾に通って対策すべきですか?
人によりますが、「対数関数など分野をわからないまま放置している人」や「一人では計画的に進めにくい人」は、塾の活用が効果的です。
数学は「わかる」と「解ける」の間に差がある科目なので、独学だけでは理解が不十分なままになってしまうことがあります。また、学校の授業だけではペースが合わなかったり、質問しにくかったりする場合もあるでしょう。
塾に通えば、以下のようなメリットがあります。
- 苦手な単元をすぐに質問できる
- 定期テストや受験に向けて計画的に学べる
- 解き方の「コツ」や「別の考え方」が学べる
- モチベーションを保ちやすい
ただし、「学校の授業で十分理解できていて、自分で演習もできている人」は、無理に通う必要はありません。重要なのは、自分に合った勉強法を見つけることです。
まずは今の状況を見て、「つまずきがあるか」「勉強のリズムが作れているか」をチェックしてみましょう。
おすすめの塾については、以下の記事で詳しく解説していますので、ぜひご覧ください。
永田先生から対数関数が苦手な高校生へメッセージ
永田先生
初めて扱う概念なので、よくわからなくて取っ付きづらいと感じることも多いでしょう。ですが、logの計算は他の単元でも登場します。ここでしっかり定義を押さえて、計算に慣れておくことが非常に重要です。実際に手を動かしてたくさん演習をすることで、計算方法を定着させましょう。頑張ってください!
まとめ 対数関数は考え方でわかる!

対数関数は、最初は「なんだか難しそう」と感じるかもしれませんが、本質はシンプルで、指数を逆から見ただけにすぎません。
log の式は、「この数を何乗したらこの値になるのか?」という問いに答える道具です。つまり、指数を「さかのぼる」ための考え方とも言えます。
難しく感じるのは、式の形やルールが見慣れないだけです。この記事で紹介したような公式やグラフの特徴、よくあるパターンをしっかり押さえておけば、丸暗記しなくても「意味から理解する」ことができます。
対数関数は将来、理系・情報・経済などの分野でも頻出の概念です。高校のうちに基本の考え方を身につけておけば、あとで必ず役に立つ場面が出てきます。
まずは、「指数の逆」という感覚をしっかり持つところから始めましょう。考え方がわかれば、対数はきっとあなたの味方になります。
執筆者プロフィール

塾選ジャーナル編集部です。『塾選ジャーナル』は、日本最大級の塾検索サイト『塾選(ジュクセン)』が提供する、教育・受験に関する総合メディアです。保護者が知っておきたい受験や進路情報をお届けします。
監修者プロフィール

2001年生まれ 東京大学教育学部卒 公立高校から学習塾に入らずに東大へ現役合格。中学・高校は野球部に所属、部活動と勉強を並行し 「練習で自分の苦手を潰して、試合で自分の力を最大限に発揮する準備をする」という努力の「型」を 勉強にも活かして受験勉強を乗り切る。得意科目は数学で、高校2年生のときに数学オリンピック本選に出場した経験がある。現在は(株)カルぺ・ディエムに所属し全国各地で年間100回以上の講演活動を行い、勉強モチベーションや計画の立て方などを伝えている。自著に、「東大生の考え型(2022,日本能率協会マネジメントセンター)」「東大式 数値化の強化書(2024,彩図社)」などがある。 X公式アカウント:https://twitter.com/nagatakosaku08












