高校数学・ベクトルとは?内積の考え方や公式をていねいに解説【東大卒監修】

「ベクトルって、何?」「なんだか難しそう……」そんなふうに感じていませんか?
ベクトルとは、「向き」と「大きさ」という2つの量を持った、数学や物理学で用いられる概念です。
ベクトルは、高校数学の中でもつまずく生徒が多い単元です。しかし、向きと長さをもった矢印というイメージさえつかめれば、一気に見通しがよくなります。
この記事では、高校2年生のときに数学オリンピック本選に出場し、学習塾に通わずに東大へ現役合格した永田耕作さん(現在はカルぺ・ディエムで講演活動を実施)監修のもとで、ベクトルの意味と定義、考え方を、図や具体例を使ってわかりやすく解説します。
編集部
塾選ジャーナル編集部
塾選ジャーナル編集部です。『塾選ジャーナル』は、日本最大級の塾検索サイト『塾選(ジュクセン)』が提供する、教育・受験に関する総合メディアです。保護者が知っておきたい受験や進路情報をお届けします。
監修者
永田耕作
2001年生まれ 東京大学教育学部卒 公立高校から学習塾に入らずに東大へ現役合格。中学・高校は野球部に所属、部活動と勉強を並行し 「練習で自分の苦手を潰して、試合で自分の力を最大限に発揮する準備をする」という努力の「型」を 勉強にも活かして受験勉強を乗り切る。得意科目は数学で、高校2年生のときに数学オリンピック本選に出場した経験がある。現在は(株)カルぺ・ディエムに所属し全国各地で年間100回以上の講演活動を行い、勉強モチベーションや計画の立て方などを伝えている。自著に、「東大生の考え型(2022,日本能率協会マネジメントセンター)」「東大式 数値化の強化書(2024,彩図社)」などがある。 X公式アカウント:https://twitter.com/nagatakosaku08

目次
ベクトルとは簡単にいうと何?

ベクトルとは、「向き」と「大きさ」という2つの量をもった、数学や物理学で用いられる概念です。
まずはこの定義だけでも覚えておきましょう。ここから、ベクトルの考え方をやさ易しく解説していきます。
「向き」と「長さ」がある矢印みたいなもの
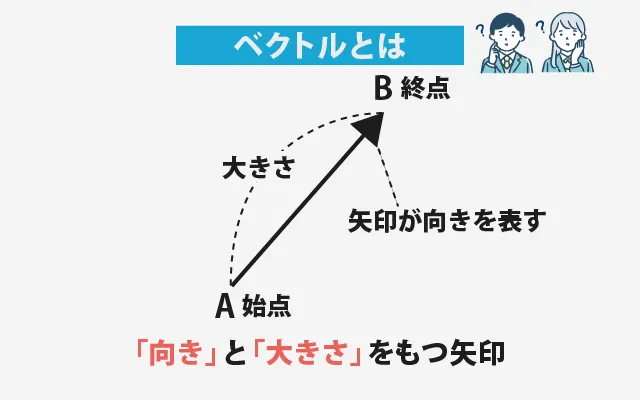
「ベクトルって難しそう……」と思っていませんか? でも、ベクトルとは「向き」と「長さ」をもった矢印のようなものだと考えると、とてもシンプルです。
例えばサッカーボールを蹴ったとき、ボールは「どの方向に」「どれくらいの速さ(強さ)」で進みますよね? このときの「ある方向」と「ある速さ」をセットで表したものが、まさにベクトルの考え方です。
- 向き → 進む方向(右、北西など)
- 長さ(大きさ) →進む量(数値で表される)
ベクトルは、日常では意識していなくても、実はスポーツ・地図・風の向きなど、身の回りのさまざまな場面で使われています。
数学では、このベクトルを使って「ものの動き」や「位置関係」などを、図や数字で正確に表現できるようにするのが目的です。
ベクトルの意味は2つある?
「ベクトル」という言葉は、実は日常と数学で少し異なる意味で使われています。
例えば「このチームはベクトルが合っていない」や「部活のベクトルをそろえよう」といった言い回しを耳にしたことがあるかもしれません。この場合のベクトルは、「考え方の方向性」や「方針の一致・不一致」といった比喩的な意味合いで使われています。人や組織の意識が同じ方向に向いているかどうかを表す表現です。
一方で数学におけるベクトルは、もっと明確な定義をもっています。数学のベクトルは、「向き」と「大きさ(長さ)」の両方をも持つ量を意味しており、矢印で表されるのが一般的です。
用語の使われ方
| 用語の使われ方 | 意味 | 例 |
|---|---|---|
| 日常会話のベクトル | 考え方や方針の方向性 | 「チームのベクトルを合わせよう」 |
| 数学のベクトル | 向きと長さをもった量(矢印) | 「→ABは右に3、上に2進むベクトル」 |
つまり、数学のベクトルは物理的な「量」を扱うのに対して、日常のベクトルは比喩的な表現なのです。
「向き(方向)」を重視している点は共通しています。
永田先生
ベクトルは、「どの方向にどれだけ進むか」を表す道案内のようなもの。堅苦しい定義を見ると難しく感じるかもしれませんが、実はとても身近な考え方なのです。
ベクトルが日常で役立っている例
数学で学ぶ「ベクトル」は、決して教科書の中だけのものではありません。実は私たちの身の回りにも、ベクトルの考え方が生かされている場面が多くあります。
例えば、サッカーや野球でボールを蹴ったり投げたりするとき、そのボールは「ある方向」に「あるスピード」で飛んでいきます。このような動きを表すとき、進む向きと、どれくらいの速さ(強さ)で動いているかの2つの情報をセットで考える必要があります。これを図に表すと、矢印1本で「向き」と「大きさ」が示されるため、とても直感的に理解しやすくなります。
また天気予報などで表示される「風向きと風速の分布図」も、ベクトルの応用例のひひとつです。地図上に示された矢印は、風がどの方向に向かって、どれくらいの強さで吹いているかをひと目で表しており、気象の現場では情報の整理や可視化に広く使われています。
永田先生
このようにベクトルを用いることで、言葉や数字だけでは把握しづらい動きや変化の向きを、視覚的かつ論理的に整理することができるのです。ベクトルは、私たちが世界を理解し、情報を整理するための有効なツールの一つといえるでしょう。
ベクトルの表し方は?

ベクトルにはいくつかの表し方があります。記号や文字の使い方に少しだけルールがありますが、一度覚えてしまえば簡単です。ここでは、ベクトルの基本的な書き方と読み方について紹介します。
ベクトルは矢印を用いて「→AB」と表す
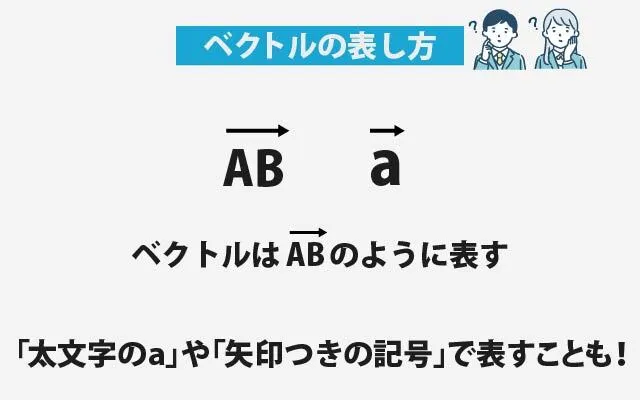
ベクトルの代表的な書き方の一つに「→AB」という表現があります。これは、点Aから点Bに向かう矢印を表していて、ベクトルの「向き」と「長さ」を意味します。
ここで重要なのは、「順番」です。始まりの点を始点、終わりの点を終点と考えます。
- 「→AB」:点Aが始まり、点Bが終わり。点Aから点Bへ向かうベクトル。
- 「→BA」:点Bが始まり、点Aが終わり。点Bから点Aへ向かうベクトル(向きが逆になる)。
つまり「→AB」と「→BA」は同じ点を使っていても、意味がまったく異なるのです。
またベクトルの「長さ」は、点Aと点Bの間の距離で決まります。
「向き」は、AからBに向かって進む方向です。
「太文字のa」や「矢印つきの記号」も出てくる
ベクトルを表記するときは、以下のような見慣れない書き方も登場します。
1. 太文字の a(ベクトルa)
印刷された教科書や問題集などでは、太字の小文字アルファベット(例:a, b, vなど)でベクトルを表すことがあります。
例:a = (3, 2)
これは「右に3、上に2進むベクトルa」という意味です。
2. 矢印つきの記号(a→)
手書きや板書、大学入試の解答などでは、文字の上に矢印をつけた表記がよく使われます。
例:a→=(3,2) = (3, 2)a=(3,2)
このように見た目は違っても意味は同じで、どちらも「ベクトルa」を表しています。つまり使い分けは状況や媒体によって変わるだけで、意味は変わらないということです。どちらの表記にも慣れておくと、テストや参考書で混乱しにくくなります。
永田先生
ベクトルの書き方はいくつか種類があるため、最初は戸惑うかもしれませんが、「どこからどこへ」という視点を持つことで、自然と読み解けるようになるはずです。
ベクトルの平行移動とは?

ベクトルの特徴の一つが、「場所に関係なく意味が変わらない」という性質です。
これは「ベクトルの平行移動」と呼ばれる考え方で、向きと長さが同じなら、どこにあっても同じベクトルとみなせるというルールです。
少し不思議に感じるかもしれませんが、実はこの考え方はとても便利です。
「向きと長さ」が同じなら、場所が違ってもOK!
数学でのベクトルは、位置が違っても「向き」と「長さ(大きさ)」が同じなら、同じものとして扱います。
この性質を「ベクトルの平行移動」といいます。
例えば以下のようなケースが該当します。
- 点Aから点Bへ向かう矢印 →AB(右に3、上に2)
- 点Cから点Dへ向かう矢印 →CD(同じく右に3、上に2)
この2本の矢印は、スタート地点も通る場所も違うのに、進む方向も長さもまったく同じです。
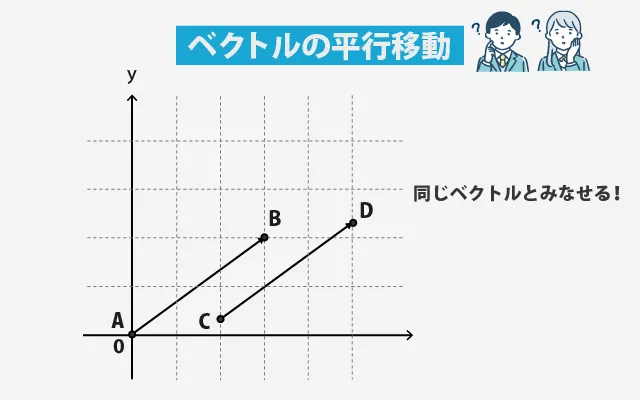
数学では、こうした矢印は「同じベクトル」とみなしてOKです。
原点スタートに置き換えられる
ベクトルの平行移動の性質を使うと、すべてのベクトルを原点(0,0)から始めた形で表すことができます。
例えば、→ABが右に3、上に2なら、「(3, 2)」という成分で書くことができるわけです。
これが次の学習テーマ「成分表示」に直結します。
ポイントまとめ
- 場所が違っても、向きと長さが同じならベクトルとしては同じ
- 原点から始めることで、ベクトルを数値で表しやすくなる
- 図形ではなく「数」で扱う準備ができる
このように、ベクトルの位置を気にせず扱えることで、計算や式への応用がしやすくなるのです。
永田先生
ベクトルは「場所に縛られない」というユニークな性質を持っています。これは図形問題を解くときにも大きな助けになるので、必ず押さえておきましょう。
ベクトルの成分表示とは?

これまでベクトルは「矢印」で表してきましたが、数学ではそれを数字(成分)で表す方法もあります。
それが成分表示と呼ばれる方法で、ベクトルを座標のような形で表すことができます。
例えば、「(3, 2)」という表記は、右に3、上に2進むベクトルを意味します。
成分表示の意味と読み方(基本)
ベクトルの成分表示「(3, 2)」は、単なる数字のペアではありません。これは、ベクトルがどの方向に、どれだけ進むかを表すものです。
具体的には、「(3, 2)」という成分には次のような意味があります。
- x方向に3進む → 横に3マス
- y方向に2進む → 上に2マス
つまり「右に3、上に2」進むベクトルを表しています。
このような成分は、原点(0, 0)から出発して、点(3, 2)まで矢印を引いたときの動きと考えるとわかりやすくなります。
成分表示は以下のように読むのが基本です。
成分表示の読み方
| ベクトル | 意味(動き方) |
|---|---|
| (3, 2) | 右に3、上に2 |
| (−2, 1) | 左に2、上に1 |
| (0, −3) | 上下方向のみ3下がる |
このように、成分は「どのくらい」「どの方向に」動くかを示す情報です。
「原点スタート」で考えるとわかりやすい
ベクトルの成分表示「(3, 2)」のような表現は、「原点スタート」で考えるとぐっとわかりやすくなります。
原点とは、座標(0, 0) のことです。グラフでいうと、横軸(x軸)と縦軸(y軸)が交わる場所が原点になります。
なぜ原点からスタートするの?
ベクトルには「位置は関係ない」という性質があるため、どこから始めても本来は問題ありません。ですが、計算や表記をシンプルにするために、すべてのベクトルを原点から始めたと考えるのが一般的です。
ベクトルを原点からの「動き」として捉えると、視覚的にも数値的にも理解しやすいのです。
どこにも動かないベクトル「(0, 0)」
これまでの例では、ベクトルは「どこかに向かって動く矢印」として紹介してきました。では、成分が (0, 0) のベクトルはどうなるのでしょうか?
「(0, 0)」とは、以下のようなベクトルであるといえます。
- x方向(横)に0
- y方向(縦)にも0
つまり、どこにも動かないベクトルです。始点と終点が同じ場所にあるため、矢印としては見えないベクトルになります。
このような「動かないベクトル」は、ゼロベクトル(または零ベクトル)と呼ばれます。
ゼロベクトルは「大きさが0で向きが定まらない」という、ちょっと特殊な存在です。
永田先生
成分表示を使えば、ベクトルを「どれだけ右と上に動くか」に読みかえることができます。この感覚を覚えておきましょう。文章よりも図を描く方が理解しやすいので、積極的に図を描いてみてください。
ベクトルの足し算・引き算は?

ベクトルは数字(成分)で計算できますが、まずは図でのイメージを理解しておくと、計算方法もすんなり頭に入ります。ここでは、ベクトルの足し算から見ていきましょう。
「足す」は矢印をつなげるイメージ
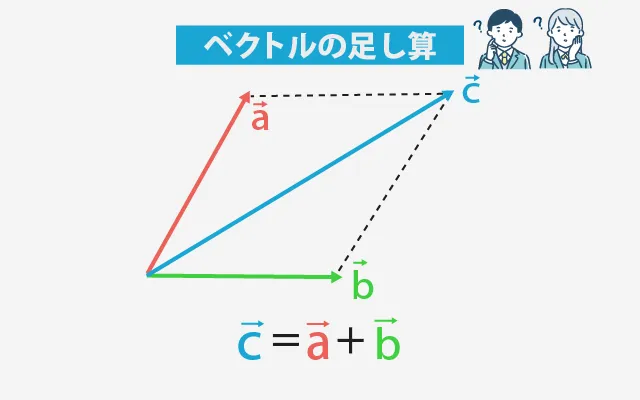
ベクトル同士の足し算は、矢印を順番につなげていくように考えます。
考え方の手順
- 最初のベクトルを描く(例:→AB)。
- 次のベクトルを、最初のベクトルの終点から描き始める。
- 最初の始点と、最後の終点を結ぶ矢印が、足し算の結果。
例えば、
- a→=(3,2)
- b→=(1,4)
の2つを足す場合は、
- 原点からa→を描く(右に3、上に2)。
- その終点からb→を描く(右に1、上に4)。
- 原点から最終地点までの矢印がa→+b→になる。
成分で計算するともっと簡単
成分表示を使えば、それぞれのx成分、y成分を足すだけで答えが出ます。
(3,2)+(1,4)=(3+1,2+4)=(4,6)
つまり、結果のベクトルは「右に4、上に6」の動きになります。
永田先生
ベクトル同士の足し算は、「矢印を順番につなげる」というイメージを持つと直感的に理解できます。最初は矢印を思い浮かべたり、実際に図に描いたりして計算し、慣れてきたら成分表示で計算する方法に移行すると効率的です。
「引く」は逆向きの矢印を足すだけ
ベクトルの引き算は、足し算の考え方を応用できます。ポイントは引くベクトルの向きを逆にして、足し算に置き換えることです。
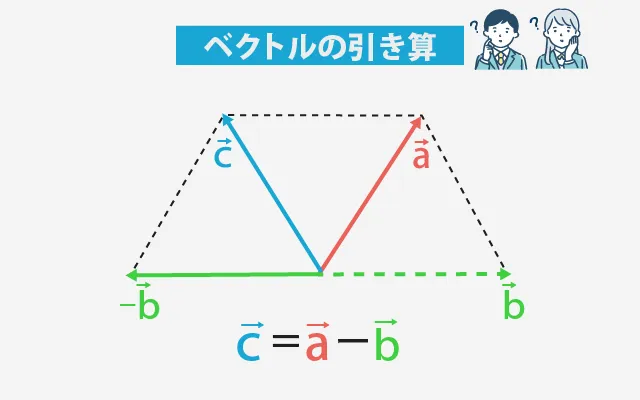
考え方の手順
- a→を描く。
- b→の向きを逆にした −b→を用意。
- a→の終点から −b→をつなげて描く。
- 始点から最終地点までの矢印が a − b になる。
成分で計算するともっと簡単
ベクトルを成分表示にすれば、引き算は単純にそれぞれの成分を引くだけです。
例:a = (3, 2)、b = (1, 4)のとき、
a − bは、
(3, 2) − (1, 4) = (3 − 1, 2 − 4) = (2, −2)
つまり、結果のベクトルは「右に2、下に2」進むベクトルになります。
ベクトルのスカラー倍
ベクトルを「2倍する」「3倍する」とは、向きはそのままで長さ(大きさ)だけを2倍、3倍にするという意味です。この操作をスカラー倍と呼びます。ここでいう「スカラー」とは、普通の数(1、2、3、0.5など)のことです。
例で考えてみよう
ベクトル a→ = (2, 1) を 3倍すると、
(2, 1) × 3 = (6, 3)
となります。これは、右に6、上に3進むベクトルです。もとの a→ と向きは同じですが、長さが3倍になっています。
永田先生
計算式だけで理解しようとせず、図にしてイメージをつかむことが大切です。「矢印のつなぎ方」に注目すれば、一気にわかりやすくなるはず。
ベクトルの内積とは?

「ベクトル同士の掛け算みたいなもの」と考えよう
ベクトルには、足し算や引き算のほかに「掛け算のような計算」もあります。これを内積と呼びます。見た目はかけ算に似ていますが、意味は少し違います。
内積の基本イメージ
内積は、2つのベクトルの向きがどれくらいそろっているかを数字で表す計算です。
- 向きが同じ → 内積は大きな正の数
- 直角(90度) → 内積は0
- 向きが反対 → 内積は負の数
つまり、内積は「ベクトル同士の方向の関係」を調べるための道具なのです。
例えば、人が台車を押している場面を想像してください。
- 台車を進む方向に押すと、しっかり前に進みます(内積が大きい)。
- 横から押しても前には進みません(内積は0)。
- 進む方向と逆に押すと、動きが止まったり後退したりします(内積は負)。
こう考えると、内積は「一方のベクトルが、もう一方の方向にどれだけ役立っているか」を測る計算だとわかります。
成分がわかれば「掛けて足す」だけで簡単!
ベクトルの成分表示がわかっている場合は、「対応する成分同士を掛けて足す」だけで内積を計算できます。

例:a→ = (3, 2)、b→ = (1, 4)のとき、内積を求めよ。
計算すると、
a→・b→ = 3 × 1 + 2 × 4 = 3 + 8 = 11
このように、成分がわかれば角度を求める必要がなく、計算が一瞬で終わります。
永田先生
「内積」はベクトルが「どれくらい同じ方向を向いているか」を測る指標です。角度やcosの意味を深く考えるとよくわからなくなってしまう場合は、まずは「掛けかけて足すだけ」という成分表示の計算ルールを覚えるところから始めましょう。
「角度×長さ×長さ」でも求められる!
ベクトル同士の内積は、角度と長さを使った公式でも求められます。この方法は図形的なイメージがしやすく、内積の意味を直感的に理解するのに向いています。
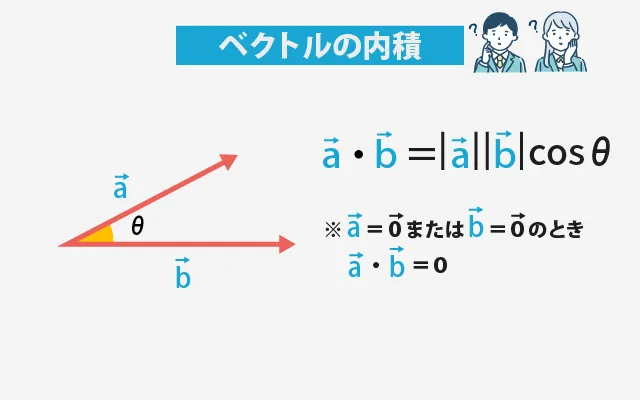
内積の公式(角度と長さを使う形)
内積 = a→ の長さ × b→ の長さ × cosθ
ここで、
- a→ の長さ:ベクトル a→ の大きさ
- b→ の長さ:ベクトル b→ の大きさ
- θ:a→ と b→ のなす角(0°〜180°)
この公式からわかること
- 角度が0°(同じ方向)なら cosθ = 1 なので、内積は長さの掛け算そのものになる。
- 角度が90°(直角)なら cosθ = 0 なので、内積は0になる。
- 角度が180°(逆方向)なら cosθ = -1 で、内積は負の値になる。
つまり、cosθ の値が方向の一致度を表し、長さの掛け算がその規模を決めると考えるとわかりやすいです。
ベクトルの練習問題にチャレンジ!【問題編】

① 成分表示の練習問題
次のベクトルを成分表示で書きなさい。
(1) 原点から右に5、上に3進むベクトル
(2) 原点から左に2、下に4進むベクトル
次のベクトルの成分を読み取りなさい。
(1) a→ = (7, 0)
(2) b→ = (−3, 2)
② ベクトルの足し算・引き算の問題
a→ = (3, 2)、b→ = (1, 4) のとき、a→ + b→ を求めなさい。
a→ = (5, −1)、b→ = (2, 3) のとき、a→ − b→ を求めなさい。
③ スカラー倍・内積のやさしい問題
a→ = (2, 1) のとき、3a→ を求めなさい。
a→ = (3, 2)、b→ = (1, 4) のとき、a→・b→(内積)を求めなさい。
④ ちょっとだけ応用(向きやゼロベクトルの確認)
a→ = (4, 2)、b→ = (8, 4) のとき、a→ と b→ の向きは同じか?
a→ = (0, 0) のとき、このベクトルの長さと向きを答えなさい。
ベクトルの練習問題にチャレンジ!【解説編】

① 成分表示の練習問題
(1) (5, 3)
(2) (−2, −4)
(1) x成分が7、y成分が0 → 横に7進むベクトル
(2) x成分が−3、y成分が2 → 左に3、上に2進むベクトル
② ベクトルの足し算・引き算の問題
(3, 2) + (1, 4) = (4, 6)
(5, −1) − (2, 3) = (3, −4)
③ スカラー倍・内積のやさしい問題
3 × (2, 1) = (6, 3)
(3, 2)・(1, 4) = 3×1 + 2×4 = 3 + 8 = 11
④ ちょっとだけ応用(向きやゼロベクトルの確認)
b→ は a→ の2倍の長さで向きも同じ → 向きは同じ
長さは0、向きは定まらない(ゼロベクトル)
永田先生
練習問題は、実際に図を描いてイメージしてから計算すると理解が深まります。特に足し算・引き算は成分表示だけでなく作図法にも慣れておくと、応用が効くのでおすすめです。
ベクトルについてよくある質問(FAQ)

ここでは、ベクトルについてよくある質問を解説します。
数学Cはいつから復活しましたか?
高校数学の科目「数学C」は、かつて存在していましたが、2003年度の学習指導要領改訂で廃止され、その内容は数学Bや数学IIIなどに分割されました。
その後、2022年度から実施された新しい学習指導要領で再び復活しました。復活した数学Cには、ベクトル・平面上の曲線と複素数平面といった分野が含まれています。
ベクトルは高校何年生で学びますか?
現在の学習指導要領では、ベクトルは**数学C**に含まれています。そのため、ベクトルを学ぶ学年は学校のカリキュラムによって異なりますが、一般的には**高校2年生または3年生**で学習するケースが多いです。
ベクトルの公式を教えてください
ここでは、高校数学でよく使うベクトルの基本公式をおさらいします。すべて a→, b→ の表記で統一しています。
ベクトルの基本公式
| 表せること | 式 |
|---|---|
| 成分表示 | a→ = (x1, y1) b→ = (x2, y2) |
| 長さ(大きさ) | √(x1² + y1²) |
| 足し算・引き算 | a→ + b→ = (x1 + x2, y1 + y2) a→ − b→ = (x1 − x2, y1 − y2) |
| スカラー倍 | k × a→ = (k × x1, k × y1) (kは実数。正なら向きは同じ、負なら向きが反対) |
| 内積 |
成分を使う方法
|
ベクトルなど数学対策に強い塾はありますか?
「ベクトルが苦手すぎる! 数学対策ができる塾に通いたい」という方は、塾のサポートを活用するのも大切な選択肢です。
ベクトルは「計算」だけでなく、「図で考える力」や「抽象的なイメージの理解」が必要になるため、一人で勉強しているとつまずきやすい単元の一つです。
また、共通テストや難関大学では図形×ベクトルの融合問題も出題されるため、早めに基本を固めておくと安心です。
おすすめの塾については、以下の記事で紹介していますので、ぜひご覧ください。
まとめ ベクトルとは向きや大きさのある量のこと!

ベクトルは、「向き」と「大きさ」をあわせ持つ量です。数学ではこれを、矢印や(3, 2)のような成分表示で表します。
向きは進む方向、大きさは進む量を意味し、物理や工学、プログラミング、AI分野など幅広い分野で使われます。
今一度、ベクトルの簡単な決まりをおさらいします。
- ベクトルの意味:向きと大きさを持った量
- 書き方:→AB、a→、(x, y) など、いくつかの表記方法がある
- 位置に依存しない性質:平行移動しても同じベクトルとして扱える
- 成分表示:原点からの横と縦の移動量で表す
- 計算方法:足し算・引き算・スカラー倍・内積など、数値として扱える
ベクトルは一見難しそうに見えますが、「向きと長さ」というシンプルな概念を理解すれば、さまざまな応用が可能です。今回の内容をきっかけに、ぜひ計算や応用にも挑戦してみてください。
執筆者プロフィール

塾選ジャーナル編集部です。『塾選ジャーナル』は、日本最大級の塾検索サイト『塾選(ジュクセン)』が提供する、教育・受験に関する総合メディアです。保護者が知っておきたい受験や進路情報をお届けします。
監修者プロフィール

2001年生まれ 東京大学教育学部卒 公立高校から学習塾に入らずに東大へ現役合格。中学・高校は野球部に所属、部活動と勉強を並行し 「練習で自分の苦手を潰して、試合で自分の力を最大限に発揮する準備をする」という努力の「型」を 勉強にも活かして受験勉強を乗り切る。得意科目は数学で、高校2年生のときに数学オリンピック本選に出場した経験がある。現在は(株)カルぺ・ディエムに所属し全国各地で年間100回以上の講演活動を行い、勉強モチベーションや計画の立て方などを伝えている。自著に、「東大生の考え型(2022,日本能率協会マネジメントセンター)」「東大式 数値化の強化書(2024,彩図社)」などがある。 X公式アカウント:https://twitter.com/nagatakosaku08












