数学Bの数列とは？基本の公式から応用問題まで東大卒ライターがやさしく解説

「数列、どう考えればいいかわからない」そのように感じていませんか？

数列とは、ルールに沿ってならんだ数の集まりのことです。

監修は、高校2年時に数学オリンピック本選に出場し、学習塾に通わずに東京大学へ現役合格した永田耕作さん（現在はカルぺ・ディエムにて教育系講演活動を展開中）。

定期テスト対策にもつながる練習問題つきで、読むだけでなく「実際に解ける力」もつく内容です。

数列とは？

数列とは、簡単にいえば「数字がルールに従って順番に並んでいるもの」です。

例えば、次のような並びもすべて数列です。

• 1, 2, 3, 4, 5（+1ずつ増える）
• 2, 4, 6, 8, 10（+2ずつ増える）
• 1, 4, 9, 16, 25（自然数の2乗の数）

このように、きちんと決まったルールに従って並んでいることが、数列のポイントです。

また、並んでいる一つひとつの数字のことを「項」と呼びます。最初の数は「第1項」、次は「第2項」というように、順番をつけて表現します。

「数列」と聞くと、教科書の中だけの話に思えるかもしれません。でも実は、数列の考え方は私たちの身のまわりにもたくさん使われています。

例えば以下のようなものも、見方を変えてみれば数列の一種といえます。

• カレンダーの日付：1日、2日、3日、…と日付が1ずつ増えていく様子は、1ずつ増える数列の例です。
• エスカレーターの段：足元を見てみると、段の高さや順番は一定の間隔で並んでいて、これも数列の考え方と同じです。

このように、数列は「数学だけの世界」ではなく、生活の中に自然に存在しているんです。身近な例からイメージをつかめると、数学の内容もぐっと身近に感じられるようになりますよ。

永田先生

「数列」と聞くと難しそうに聞こえるかもしれませんが、実は「数が並んでいるだけ」のものです。
数字一つひとつに注目するよりも、その関係、つまり「並び方」に目を向けると、ずっとわかりやすくなります。

これだけは押さえよう！数列の種類

ここでは、高校数学で必ず出てくる重要な数列の種類をやさしく紹介します。

種類といっても難しく考える必要はありません。「どんなルールで数字が並んでいるか」に注目すれば、すんなり理解できます。

等差数列（毎回同じ数を足す）

等差数列とは、数字が毎回同じ数だけ増えていく数列のことです。「足す数」がずっと同じなので、足し算のパターンとして覚えるとイメージしやすくなります。

例えば、このような数列が該当します。

• 2, 5, 8, 11, 14…

この数列では、どの数字も「前の数に+3」すると次の数が出てきます。

• 5 = 2 + 3
• 8 = 5 + 3
• 11 = 8 + 3
• 14 = 11 + 3

このように、増え方がずっと同じ＝等しい差になっているから「等差数列」と呼ばれます。

等差数列では、「何番目の項（＝第n項）」がいくつになるかを公式でパッと求めることができます。このときに使うのが 「一般項（いっぱんこう）」の公式です。

公式は次のようになります。

aₙ = a₁ + (n - 1) × d

• aₙ：n番目の項
• a₁：最初の項（第1項）
• d：差（毎回足している数）

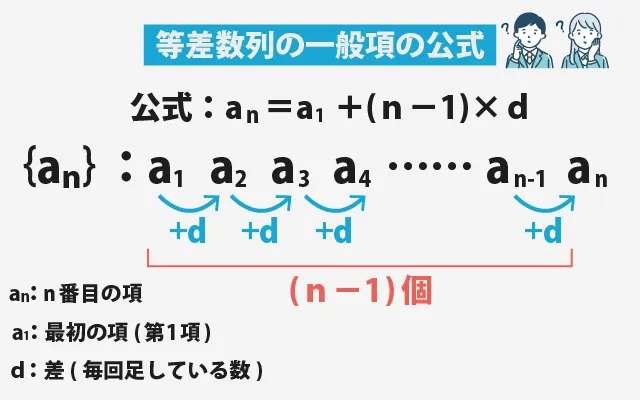
先ほどの2, 5, 8, 11, 14…,という数列に当てはめてみましょう。このとき、a₁ = 2、d = 3 なので、一般項はaₙ = 2 + (n - 1) × 3となります。

永田先生

「一般項」という言葉は難しそうに聞こえますが、言い換えると「n番目の数は何か？」を求める式のことです。そう考えるとシンプルでわかりやすいでしょう。
一般項は、1つずつ数えていくよりも、n番目まで計算で簡単にたどり着ける「数学的ショートカット」なんです。

等比数列（毎回同じ数をかける）

等比数列（とうひすうれつ）とは、数字が毎回“同じ数をかけて”増えていく（または減っていく）数列のことです。先ほどの「等差数列」が足し算の数列だったのに対して、等比数列はかけ算の数列です。

例えば、このような数列が該当します。

• 3, 6, 12, 24, 48…

この数列では、前の数に毎回「×2」すると次の数が出てきます。

• 6 = 3 × 2
• 12 = 6 × 2
• 24 = 12 × 2
• 48 = 24 × 2

このように、「かける数（比）」がずっと同じなので「等比（＝同じ比率）」数列と呼ばれます。

等比数列でも、n番目の項を一発で求められる公式（＝一般項）があります。

公式はこうなります。

aₙ = a₁ × r⁽ⁿ⁻¹⁾

• aₙ：n番目の項
• a₁：最初の項（第1項）
• r：毎回かける数（＝「公比」）

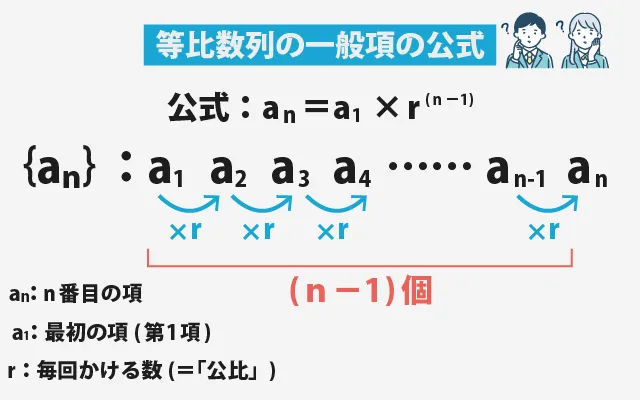
先ほどの3, 6, 12, 24, 48…という数列に当てはめてみましょう。このとき、a₁ = 3、r = 2 なので、一般項はaₙ = 3 × 2⁽ⁿ⁻¹⁾となります。

永田先生

等比数列は、公比が1よりも大きいとき、「どんどん加速する増え方」をするところが面白いポイントです。
rの値が大きければ大きいほど、初項が小さくても、すぐに大きな数になります。

階差数列（変化の変化を見る）

階差数列は、一見するとバラバラに見える数の並びでも、「差」を見ていくと実はルールが隠れているというタイプの数列です。

例えば、このような数列が該当します。

1, 4, 9, 16, 25…

この並び、一見すると等差でも等比でもなさそうですよね。でも、隣り合う数の差（階差）を見てみるとこうなります。

• 4 - 1 = 3
• 9 - 4 = 5
• 16 - 9 = 7
• 25 - 16 = 9

なんと、「差が +2ずつ増えている」ことがわかります。つまり、この「差の並び」も等差数列になっているのです！

元の数列の増え方の増え方に注目することで、「ルールが見えなかった数列」も実は規則的だったと気づくことができます。

このように、1段階目の差を見てパターンを発見する数列を「階差数列」と呼びます。

永田先生

階差数列と聞くとピンと来ないかもしれませんが、実はパズルみたいな面白い数列なんです。
最初は規則が見えなくても、差同士の「差」をとってみると意外な発見があるかもしれません。

数列の和とは？

「数列の和」と聞くと、「え、なんだか難しそう」と感じるかもしれません。でも、言葉をかみ砕いてみると、ただの足し算のことなんです。

この章では、まず「和ってなに？」という基本からスタートし、等差数列・等比数列の和の求め方まで、図を交えてわかりやすく紹介していきます。

「和」とは数列のいくつかの項を足したもの

「和」とは、数列のいくつかの項（数）を足したもののことです。つまり、「数列の合計」を求めることが和を出すという意味になります。

例えば、以下のような数列を考えてみましょう。

1, 2, 3, 4, 5

この数列の和は、次のように計算します。

1 + 2 + 3 + 4 + 5 = 15

とてもシンプルですよね。「順番に並んだ数を足す」= 数列の和です。

永田先生

「数列の和」というと身構えてしまう人が多いのですが、実はただの「合計」です。
公式をただ使う前に、まずは「足しているだけ」ということを意識しましょう。
イメージしながら基本を押さえることが、応用への一番の近道です。

等差数列の和はルールで求められる！

等差数列では、「毎回同じ数を足している」ことがポイントでしたね。この特徴を使うと、和＝合計を、あるルール（公式）を使ってサッと計算することができます。

先ほど

1 + 2 + 3 + 4 + 5 = 15

という計算を紹介しましたが、1〜100 まで全部足すときは大変ですよね。

ここで便利なのが、等差数列の和の公式です！

等差数列の和の公式は以下のような式です。

Sn =1/2 (a₁ + aₙ)n

• Sn：n項までの和（sumのS）
• a₁：最初の項
• aₙ：最後の項（n番目の項）
• n：項の数（項がいくつあるか）

では実際に、1から100までの合計を、公式を使って求めてみましょう。

この数列は1, 2, 3, 4, … , 100と続きますから、

• 最初の項 a₁ = 1
• 最後の項 a₁₀₀ = 100
• 項数 n = 100

公式に当てはめると

• Sn = 1/2(1 + 100) × 100 = 1/2 × 101 × 100 = 1/2 ×10,100 = 5,050

永田先生

100個も続いている数の和を、たった1回の計算で出すことができる。これが「公式の力」です。
単に「暗記」するだけでなく、「どうしてその公式が出てくるのか」「どんなときに使うのか」をイメージで理解しておくと、応用も効きやすくなります。

等比数列の和は不思議な特徴を持つ

等比数列は、「毎回同じ数をかけていく」数列でしたね。そのため、数字が急に大きくなったり、逆にどんどん小さくなったりするという特徴があります。

以下のような数列の和を考えてみましょう。

1, 2, 4, 8, 16

これは、「×2」ずつ増えていく等比数列です。全部足すと31になります。

等比数列の和にも、ちょっと不思議で面白いルールがあるんです。等比数列の和の公式は以下のような式です。

Sn = a × (1 - rⁿ) ÷ (1 - r) ※ ただし、r ≠ 1（分母がゼロになってしまうため）

• Sn：n項までの和
• a：最初の項（a₁）
• r：かける数（公比）
• n：項数

さっきの例を使って考えてみましょう。

1, 2, 4, 8, 16という数列の最初の項a は 1,かける数 r は 2,項の数 n は 5です。そのため、

Sn = 1 × (1 - 2⁵) ÷ (1 - 2) = (1 - 32) ÷ (1 - 2) = (-31) ÷ (-1) = 31

合計は 31！ 計算でしっかり合ってます！

永田先生

「増え方や減り方が激しい」けれど、「かけ方は一定」というのが、等比数列の面白いポイントです。
数が爆発的に増えるだけでなく、逆にどんどん小さくなることもあります。
こうして、数の世界が両方に広がっていくのは、等比数列の魅力ともいえるでしょう。

数列の漸化式とは？

「数列の一般項は公式で求められる」と学んできましたが、実は“次の項を前の項から作る”という方法もあります。それがここで紹介する「漸化式（ぜんかしき）」です。

「難しそう…」と思うかもしれませんが、やっていることはとてもシンプル！ ここでは漸化式の考え方を、やさしく・身近な例えを使って解説していきます。

漸化式とは、1つ前の項を使って次を求める式

漸化式とは、「前の項の値をもとにして、次の項を計算する式」のことです。

例えば、このような漸化式があります。

a₁ = 2

aₙ₊₁ = aₙ + 3

この式は、「最初の項は2で、次の項は“1つ前に3を足したもの”になる」というルールを表しています。

順に項を出していくと、

• a₁ = 2
• a₂ = a₁ + 3 = 2 + 3 = 5
• a₃ = a₂ + 3 = 5 + 3 = 8
• a₄ = a₃ + 3 = 8 + 3 = 11

このように、スタートの値と増え方だけで、どんどん先の項を作っていけるのが漸化式です。

永田先生

漸化式は、「1つ前の数」をもとにして次の数を作る仕組みです。
難しそうに見えても、やっていることは意外とシンプル。「前とどう違うか」「どう変形して次に進んでいるか」に注目すると、スッと理解できます。
また、一般項は「n番目を一発で求める式」、漸化式は「1つ前との関係を表す式」です。
この2つの使い方の違いも意識して覚えておきましょう。

漸化式のイメージ

漸化式のイメージとしては、「1段ずつ、2ずつ登っていく階段」のようなものです。

• 1段目：1
• 2段目：1 + 2 = 3
• 3段目：3 + 2 = 5
• 4段目：5 + 2 = 7

前の高さ（項）に決まった高さ（差）を足していくイメージです。

もう一つのイメージは、ブロックのように1つずつ積んでいくこと。「次の形は、前の形に新しいパーツを足したもの」、漸化式は、数列を手作業で作るような視点なんです。

数列の「永遠のルール」を証明！数学的帰納法とは？

数列を学んでいくと、「このルール、本当にどこまでも成り立つの？」と感じることがあるかもしれません。

そのようなときに使われるのが、数学的帰納法という証明の考え方です。

数学的帰納法とは、まず最初のステップ（n = 1など）が正しいことを示し、その次のステップ（n → n+1）でも正しいと示すことで、「すべての自然数nに対して命題が成り立つ」と結論づける証明方法です。

難しく考える必要はありません。ここでやさしく解説していきます。

ドミノ倒しで理解する！帰納法の2ステップ

数学的帰納法は、簡単にいうと

という論理の流れです。

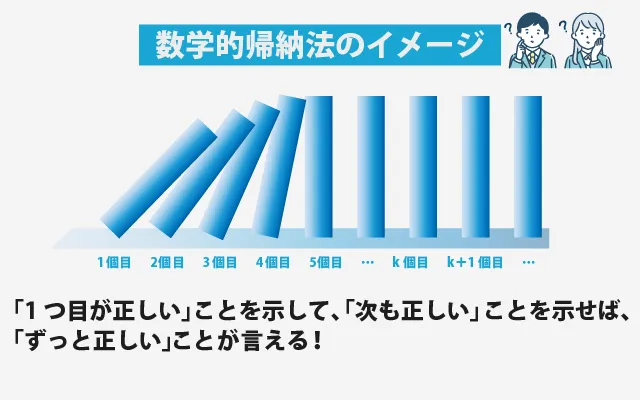
数学的帰納法の代表的なたとえが、「ドミノ倒し」です。

• 1枚目のドミノ（第1項）が倒れる（＝最初に正しい）
• 倒れたら、隣のドミノも必ず倒れる（＝次も正しい）
• …ということは、すべてのドミノが倒れる（＝すべての項で正しい）

このように、最初と次のつながりを証明できれば、無限に続く数列でも「常に成り立つ」と言えるわけです。

1. スタートの証明（初期条件）

まず確認するのは、「第1項でその主張が本当に正しいかどうか」です。

いくらルールが正しく見えても、最初が間違っていたら、全体も崩れてしまいますよね。

だからこそ、スタート地点のチェックがとても大事です。

例えば、証明したい式が以下のようなものであるとします。

1 + 2 + 3 + … + n = n(n + 1) ÷ 2

このとき、n = 1 のときに本当に合っているかを確かめます。

左辺：1

右辺：1(1 + 1) ÷ 2 = 2 ÷ 2 = 1

左右が同じなので、初期条件が満たされているということになります。

2. 連鎖の証明

次にやるのは、「n番目で正しいなら、n+1番目も正しいか？」を確認するステップです。

イメージとしては、「1枚目のドミノが倒れたら、2枚目も倒れる」という確認です。

• n = k でその主張が正しいと仮定（＝帰納法の仮定）
• それを使って、n = k + 1 のときにも同じ主張が成り立つかを数式で示します。

このステップがクリアできれば、「どのドミノが来ても、ちゃんと次に倒れる」という連鎖が完成します。

そして、無限に続く数列のすべての項でその主張が正しいことが証明されたことになるのです。

永田先生

「全部のケースで正しいことを示す」と聞くと難しそうですが、数学的帰納法はとても素直でシンプルな考え方です。慣れるまではドミノ倒しのイメージを毎回思い出しながら問題を解いてみましょう。

数列の和を証明！数学的帰納法の使い方（例題）

では実際に、数学的帰納法がどう使われるのかを、具体的な数列の例で見てみましょう。

証明したい内容（命題）

1 + 2 + 3 + … + n = n(n + 1) ÷ 2

この式は「1からnまでの和を出す式」でしたね。これがすべての自然数nで成り立つことを、数学的帰納法で証明してみましょう。

ステップ①：初期条件（n = 1）の確認

まず、n = 1 のときに式が成り立つかチェックします。

• 左辺：1
• 右辺：1(1 + 1) ÷ 2 = 2 ÷ 2 = 1

→ 左辺 = 右辺 なのでOK！

初期条件はクリアしたといえます。

ステップ②：「n = k で正しい」と仮定する

次に、ある自然数 k で式が正しいと仮定します。

1 + 2 + … + k = k(k + 1) ÷ 2

これを「仮定（かてい）」として使います。

ステップ③：n = k + 1 のときも正しいか調べる

次に、n = k + 1 のときに同じ式が成り立つかどうかを見ていきます。

左辺は

• 1 + 2 + … + k + (k + 1)
• = [ここまでの和] + (k + 1)
• = k(k + 1) ÷ 2 + (k + 1) ← さっきの仮定を使う

この式をまとめると

• k(k + 1)/2 + (k + 1)
• = (k(k + 1) + 2(k + 1)) ÷ 2
• = (k + 1)(k + 2) ÷ 2

つまり、1 + 2 + … + (k + 1) = (k + 1)(k + 2) ÷ 2と表せます。

これはまさにn(n + 1) ÷ 2 の n = k + 1 のバージョンといえます。

結論：すべての自然数nで式は正しい

以上により、

n = 1で正しい

n = kで正しいなら、n = k + 1でも正しい

という2ステップが証明できたので、数学的帰納法によりこの式はすべてのnで成り立つことがわかりました！

永田先生

帰納法は「1つできた」→「次もできる」→「全部OK！」という流れで、無限に続く数列の正しさを一気に証明してくれる、とても便利な証明方法です。
第1項で成り立つことを示したら、次はn=kで成り立つと「仮定」して、n=k+1で成り立つかどうか考える。この3ステップをしっかり押さえておきましょう。

数列の練習問題にチャレンジ！【問題編】

ここからは、実際にあなた自身の手で解いてみる問題編です！

今まで学んできた「数列の見方」「和の求め方」「漸化式」などをもとに、シンプルな問題からちょっとひねった問題までに挑戦してみましょう。

「できるかな…」と不安に思っても大丈夫。まずは考えてみること自体が、最大の学びです！

① 並び方を見て、次の数を考えよう

次の数列を見て、次に来る数を予想してみましょう。

【問題1】

5, 10, 15, 20, ( ？ )

【問題2】

1, 2, 4, 8, ( ？ )

② 和を求めてみよう

等差・等比数列の和を公式で求めてみましょう。

【問題3】

次の数列の合計を求めてください。

3, 6, 9, 12, 15

【問題4】

次の等比数列の5項までの合計を求めましょう

1, 2, 4, 8, 16

③ 差に注目してルールを発見

次の数列を見て、次に来る数を予想してみましょう。

【問題5】

2, 6, 12, 20, 30, ( ？ )

④ 漸化式のルールで続きを考えよう

「前の項から次の項を作る」漸化式を使って、続きを求める力を試してみましょう。

【問題6】

a₁ = 2, aₙ₊₁ = aₙ + 5

→ a₂, a₃, a₄ を求めてみよう

【問題7】

a₁ = 1, a₂ = 1, aₙ₊₂ = aₙ₊₁ + aₙ

→ a₃, a₄, a₅ を求めてみよう

数列の練習問題にチャレンジ！【解説編】

それでは、先ほどの問題の答え合わせ＆解説に進みましょう！ 「なぜそうなるのか？」という理由までセットで理解できるように説明していきます。

① 並び方を見て、次の数を考えよう

【問題1】

5, 10, 15, 20, (？)

→ 答え：25

毎回 「+5」ずつ増えている等差数列です。

つまり、20 + 5 = 25 になります。

【問題2】

1, 2, 4, 8, (？)

→ 答え：16

毎回 「×2」 になっている等比数列ですね。

8 × 2 = 16 です！

② 和を求めてみよう

【問題3】

3, 6, 9, 12, 15

→ 答え：45

この数列は、初項 a₁ = 3、末項 a₅ = 15、項数 n = 5 の等差数列。

和の公式を使うと

S = (a₁ + aₙ) × n ÷ 2 = (3 + 15) × 5 ÷ 2 = 18 × 5 ÷ 2 = 90 ÷ 2 = 45

となります。

【問題4】

1, 2, 4, 8, 16

→ 答え：31

等比数列なので、a = 1、r = 2、n = 5 として公式を使います。

S = a × (1 - rⁿ) ÷ (1 - r) = 1 × (1 - 2⁵) ÷ (1 - 2) = (1 - 32) ÷ (-1) = -31 ÷ (-1) = 31

③ 差に注目してルールを発見

【問題5】

2, 6, 12, 20, 30, (？)

→ 答え：42

差に注目すると、以下のようになります。

• 6 - 2 = 4
• 12 - 6 = 6
• 20 - 12 = 8
• 30 - 20 = 10

→ 差が +2ずつ増えている＝差の数列が等差数列となっています。

次の差は +12となることから、30に12を足して42が答えとなります。

④ 漸化式のルールで続きを考えよう

【問題6】

a₁ = 2、aₙ₊₁ = aₙ + 5

→ a₂, a₃, a₄ = ？

→ 答え：a₂ = 7、a₃ = 12、a₄ = 17

毎回 +5 していくだけですね。

• a₂ = 2 + 5 = 7
• a₃ = 7 + 5 = 12
• a₄ = 12 + 5 = 17

【問題7】

a₁ = 1、a₂ = 1、aₙ₊₂ = aₙ₊₁ + aₙ

→ a₃, a₄, a₅ = ？

→ 答え：a₃ = 2、a₄ = 3、a₅ = 5

• a₃ = a₂ + a₁ = 1 + 1 = 2
• a₄ = a₃ + a₂ = 2 + 1 = 3
• a₅ = a₄ + a₃ = 3 + 2 = 5

となります。

これは有名なフィボナッチ数列と呼ばれる数列です。フィボナッチ数列については、後ほど詳しく解説します。

永田先生

「答えが合っているかどうか」だけではなく、「考え方」が合っているかどうかも確認するようにしましょう。今回のように、数列にはさまざまなルールや視点があります。
それらを生かしてパターンに気づく力は、きっと日常生活でも大いに役立つはず。

数列についてよくある質問（FAQ）

ここでは、数列についてよくある質問を解説します。

数列は高校何年生で学びますか？

数列は、高校数学の「数学B」という科目の中で扱われます。学習のタイミングは学校によって異なりますが、一般的には高校2年生で学ぶことが多いです。

学校によっては、高1の終わりごろに軽く触れることもありますが、本格的に出てくるのは「数列」「ベクトル」「確率分布」などを扱う数Bの中盤〜後半です。

フィボナッチ数列とは何ですか？

フィボナッチ数列とは、前の2つの数を足して次の数を作っていく数列のことです。

最初の2つは「1, 1」から始まり、次の数はその2つの合計。以降も同じように、直前の2つを足して進んでいきます。

1, 1, 2, 3, 5, 8, 13, 21, 34, …

• 1 + 1 = 2
• 1 + 2 = 3
• 2 + 3 = 5
• 3 + 5 = 8

…というように続いていきます。

フィボナッチ数列は、単なる数学の話にとどまらず、自然界や芸術にもたくさん登場します。

例えば、ヒマワリの種の並び方にも見られます。中心から外側に広がる種の配置は、フィボナッチ数に従って渦巻き状になっていることが多いです。

永田先生

フィボナッチ数列は、「足し算だけ」で作られているのに、美しさを持つ「不思議な数列」です。
ルールはシンプルなのに奥が深い、まさに数列の代表格ともいえます。
また、自然界とのつながりを知ると、数学がぐっと身近に感じられるはずです。
ヒマワリを見つけたとき、実際に確認してみてください。

数列など数学対策に強い塾はありますか？

「数列がよくわからない」そんなふうに感じている方は、塾のサポートを活用するのがおすすめです。

数学が苦手といっても、つまずいているポイントや理解できていない原因は人それぞれです。だからこそ、自分に合った学習方法や解説の仕方で取り組むことが、理解の第一歩になります。

数学に強い塾に行けば、以下のようなメリットが期待できます。

• わからないところをピンポイントで教えてもらえる
• 自分のペースで何度も復習できる
• 「何をどう勉強したらいいか」が明確になる
• 自信を持って問題に取り組めるようになる

数学に強い塾・個別指導塾について、詳しく知りたい方は以下の記事をご覧ください。

【2025年最新版】数学の成績UPを叶える数学塾21選｜選び方や費用、口コミで徹底比較

まとめ 数列とは規則的な数の並び！

等差数列・等比数列・階差数列の仕組み、和の求め方、漸化式や数学的帰納法まで、さまざまな角度から数列を学んできました。

• 数列は、ただの数字の並びではなく、規則（ルール）に従って並んだ数の集まり
• 一つひとつの数は「項（こう）」と呼ばれ、並び方によっていろいろな種類がある
• 「どう並んでいるのか？」に気づくことが、数列の楽しさと学びの第一歩

焦らずに、基本をしっかり押さえれば、必ず理解が深まります。自信を持って進んでいきましょう！

永田先生

数列が難しくてつまずいている人も、苦手意識を持っている人も、基礎に立ち返って定義や種類、それぞれの特徴を丁寧に追っていけば、必ずできるようになります。
そのとき、ただ公式を覚えるだけでなく、なぜそうなるの？と疑問を持ち、具体例をイメージしながら勉強することが大切です。

そのほかの数学関連記事

そのほかの数学に関する記事はこちらからご覧いただけます。

中学数学の因数分解の解き方｜やり方の流れとテクニックを解説三平方の定理（ピタゴラスの定理）とは？一瞬で解ける裏ワザも紹介三角関数をわかりやすく解説！図解でスッキリわかる入門講座【東大卒監修】